
科目: 来源: 题型:
【题目】如图,已知点A是双曲线y= ![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= ![]() (k<0)上运动,则k的值是
(k<0)上运动,则k的值是 
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=4,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠DGC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在BC上,且四边形AEFD是平行四边形.
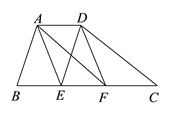
(1)AD与BC有何等量关系?请说明理由;
(2)当AB=DC时,求证:四边形AEFD是矩形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点A是双曲线y= ![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= ![]() (k<0)上运动,则k的值是
(k<0)上运动,则k的值是 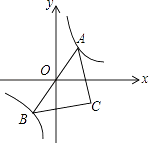
查看答案和解析>>
科目: 来源: 题型:
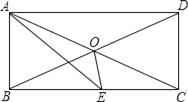
【题目】矩形ABCD中,AC、BD相交于O,AE平分∠BAD交BC于E.
(1)求证:△ABE是等腰直角三角形;
(2)若∠CAE=15°,求证:△ABO是等边三角形;
(3)在(2)的条件下,求∠BOE的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的材料:
如图①,在△ABC中,试说明∠A+∠B+∠C=180°.
分析:通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 ![]() .
.
其中正确的结论有( )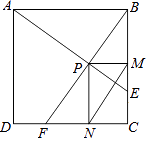
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 ![]() .
.
其中正确的结论有( )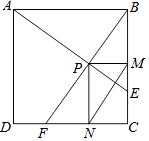
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目: 来源: 题型:
【题目】根据你的经验,分别求下列事件的概率:
(1)在一个不透明的袋中装有红球3个,白球2个,黑球1个,每种球除颜色外其余都相同,摇匀后随机地从袋中取出1个球,取到红球的概率.
(2)投掷一枚普通正方体骰子,出现的点数为7的概率.
(3)投掷两枚普通硬币,出现两个正面的概率.
查看答案和解析>>
科目: 来源: 题型:
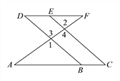
【题目】如图,E点为DF上的点,B为AC上的点,![]() ,
,![]() ,求证:DF∥AC.
,求证:DF∥AC.
证明:∵ ![]() (已知),∠1=∠3,∠2=∠4( ),
(已知),∠1=∠3,∠2=∠4( ),
∴∠3=∠4(等量代换).
∴__________![]() __________( ).
__________( ).
∴∠C=∠ABD( ).
∵∠C=∠D( ),
∴∠D=__________( ).
∴AC∥DF( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com