
科目: 来源: 题型:
【题目】如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:

(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.
查看答案和解析>>
科目: 来源: 题型:
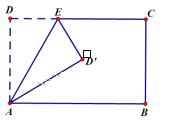
【题目】如图,矩形ABCD中,AB=8,AD=5,点E![]() 为DC边上一个动点,把△ADE沿AE折叠,点D的对应点D’落在矩形ABCD的对称轴上时,DE的长为____________.
为DC边上一个动点,把△ADE沿AE折叠,点D的对应点D’落在矩形ABCD的对称轴上时,DE的长为____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,OA是⊙O的半径,BC是⊙O的弦,且BC⊥OA,过BC的延长线上一点D作⊙O的切线DE,切点为E,连接AB,BE,若∠BDE=52°,则∠ABE的度数是( ) 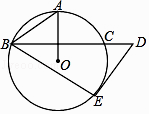
A.52°
B.58°
C.60°
D.64°
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目: 来源: 题型:
【题目】一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1小时后与摩托车相遇,此时距B地40千米.其中正确结论的个数是( )
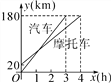
A. 2个 B. 3个 C. 4个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石.某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
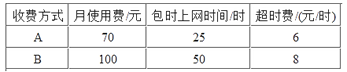
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元、yB元.
(1)当x≥50时,分别求出yA、yB与x之间的函数表达式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,E是AB边的中点,F在AD边上,M,N分别是CD,BC边上的动点,若AB=AF=2,AD=3,则四边形EFMN周长的最小值是( ) 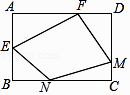
A.2+ ![]()
B.2 ![]() +2
+2 ![]()
C.5+ ![]()
D.8
查看答案和解析>>
科目: 来源: 题型:
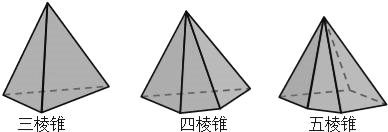
【题目】设棱锥的顶点数为V,面数为F,棱数为E.
(1)观察与发现:三棱锥中,V3= ,F3= ,E3= ;
五棱锥中,V5= ,F5= ,E5= ;
(2)猜想:①十棱锥中,V10= ,F10= ,E10= ;
②n棱锥中,Vn= ,Fn= ,En= ;(用含有n的式子表示)
(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系: ;
②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:E= ;
(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间是否也存在某种等量关系?若存在,试写出相应的等式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com