
科目: 来源: 题型:
【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点A B. 点B
C. A,B之间 D. B,C之间
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角坐标系中,点A在函数 ![]() 的图象上,AB⊥
的图象上,AB⊥ ![]() 轴于点B,AB的垂直平分线与
轴于点B,AB的垂直平分线与 ![]() 轴交于点C,与函数
轴交于点C,与函数 ![]() 的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )
的图象交于点D。连结AC,CB,BD,DA,则四边形ACBD的面积等于( )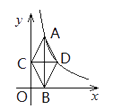
A. 2
B.![]()
C.4
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在平面直角坐标系xOy中,已知点A(0,3),B(2,3),OC=a.将梯形ABCO沿直线y=x折叠,点A落在线段OC上,对应点为E.
(1)求点E的坐标;
(2)①若BC∥AE,求a的值;(提示:两边互相平行的四边形是平行四边形,平行四边形的对边相等)
②如图②,若梯形ABCO的面积为2a,且直线y=mx将此梯形面积分为1∶2的两部分,求直线y=mx的函数表达式.
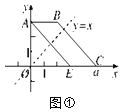
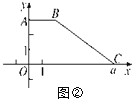
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y= ![]() x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.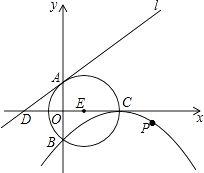
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知射线CB∥OA,∠C=∠OAB,
(1)求证:AB∥OC;
(2)如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.


查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
科目: 来源: 题型:
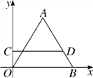
【题目】如图,平面直角坐标系中有等边△AOB,点O为坐标原点,OB=2![]() ,平行于x轴且与x轴的距离为1的线段CD分别交y轴、AB于点C,D.若线段CD上点P与△AOB的某一顶点的距离为
,平行于x轴且与x轴的距离为1的线段CD分别交y轴、AB于点C,D.若线段CD上点P与△AOB的某一顶点的距离为![]() ,则线段PC(PC<2.5)的长为____________.
,则线段PC(PC<2.5)的长为____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A. 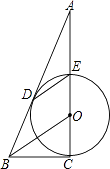
(1)求证:直线BC是⊙O的切线;
(2)若AE=2,tan∠DEO= ![]() ,求AO的长.
,求AO的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ()元;②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com