
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G.点F是CD上一点,且满足 ![]() =
= ![]() ,连接AF并延长交⊙0于点E.连接AD,DE,若CF=2,AF=3.给出下列结论:
,连接AF并延长交⊙0于点E.连接AD,DE,若CF=2,AF=3.给出下列结论:
①△ADF∽△AED;②FG=2;③tan∠E= ![]() ;④S△DEF=4
;④S△DEF=4 ![]() .
.
其中正确的是( )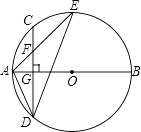
A.①②④
B.①②③
C.②③④
D.①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC的面积是60,请完成下列问题:
(1)如图①,若AD是△ABC的BC边上的中线,则△ABD的面积 _△ACD的面积(选填“>”“<”或“=”).
(2)如图②,若CD,BE分别是△ABC的AB,AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y,由题意得:S△ABE=![]() S△ABC=30,S△ADC=
S△ABC=30,S△ADC=![]() S△ABC=30,可列方程组为: ,通过解这个方程组可得四边形ADOE的面积为 .
S△ABC=30,可列方程组为: ,通过解这个方程组可得四边形ADOE的面积为 .
(3)如图③,AD∶DB=1∶3,CE∶AE=1∶2,请你计算四边形ADOE的面积,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L,K,C的投影中,与字母N属同一种投影的有( ) 
A.L,K
B.C
C.K
D.L,K,C
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,图①、图②分别由两个长方形拼成,其中a>b.
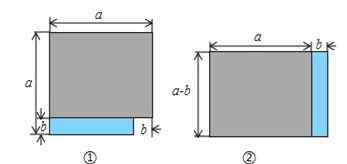
(1)用含a、b的代数式表示它们的面积,则S①= ,S②= + ;
(2)S①与S②之间有怎样的大小关系?请你解释其中的道理;
(3)请你利用上述发现的结论计算式子:20182-20172.
查看答案和解析>>
科目: 来源: 题型:
【题目】完成下列填空:
已知:如图,AB∥CD,∠B=120°,CA平分∠BCD.求证:∠1=30°.
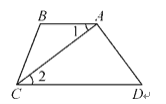
证明:∵AB∥CD( ),
∴∠B+∠BCD= ( ).
∵∠B= ( ),
∴∠BCD= ( ).
又∵CA平分∠BCD( ),
∴∠2= ( ).
∵AB∥CD( ),
∴∠1= =30°( ).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2…∠A2 017BC和∠A2 017CD的平分线交于点A2 018,则∠A2 018=_____度.
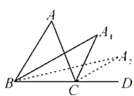
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动,已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG,设E点移动距离为x(x>0).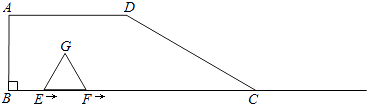
(1)△EFG的边长是(用含有x的代数式表示),当x=2时,点G的位置在;
(2)若△EFG与梯形ABCD重叠部分面积是y,求y与x之间的函数关系式;
(3)探究(2)中得到的函数y在x取何值时,存在最大值?并求出最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】基本模型:如图1,点A,F,B在同一直线上,若∠A=∠B=∠EFC=90°,易得△AFE~△BCF. 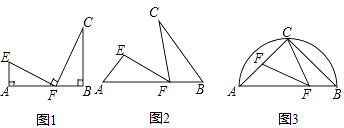
(1)模型拓展:如图2,点A,F,B在同一直线上,若∠A=∠B=∠EFC,求证:△AFE~△BCF;
(2)拓展应用:如图3,AB是半圆⊙O的直径,弦长AC=BC=4 ![]() ,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com