
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠D=90°,∠BAD=105°,在BC,CD上分别找一点M、N,使得△AMN周长最小,则∠AMN+∠ANM的度数为 ( )

A. 100° B. 105° C. 120° D. 150°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF= ![]() AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有条.
AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有条. 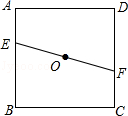
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、DQ、CQ、BQ,设AP=x.
(1)BQ+DQ的最小值是_______,此时x的值是_______;
(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.
①求证:点E是CD的中点; ②求x的值.
(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x的值.
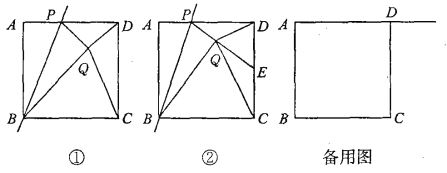
查看答案和解析>>
科目: 来源: 题型:
【题目】课间休息时小明拿着两根木棒玩,小华看到后要小明给他玩,小明说:“较短木棒AB长40cm,较长木棒CD长60cm,将它们的一端重合,放在同一条直线上,此时两根木棒的中点分别是点E和点F,则点E和点F间的距离是多少?你说对了我就给你玩”聪明的你请帮小华求出此时两根木棒的中点E和F间的距离是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论: ①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个互异实根.
其中正确结论的个数是( )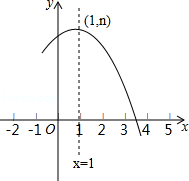
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小是( ) 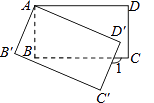
A.68°
B.20°
C.28°
D.22°
查看答案和解析>>
科目: 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,等腰直角三角形ACB与ECD的顶点都在网格点上,点N、M分别为线段AB、DE上的动点,且BN=EM. (Ⅰ)如图①,当BN= ![]() 时,计算CN+CM的值等于
时,计算CN+CM的值等于 ![]()
(Ⅱ)当CN+CM取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段CN和CM,并简要说明点M和点N的位置是如何找到的(不要求证明).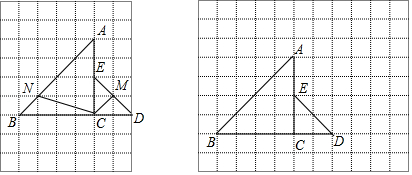
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,射线OM上有三点A、B、C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O出发,沿OM方向以1cm/秒的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动,两点同时出发,当点Q运动到点O时,点P、Q停止运动.
(1)若点Q运动速度为2cm/秒,经过多长时间P、Q两点相遇?
(2)当P在线段AB上且PA=3PB时,点Q运动到的位置恰好是线段AB的三等分点,求点Q的运动速度;
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(﹣3,0),点B坐标为(1,0),点C在y轴的正半轴,且∠CAB=30°.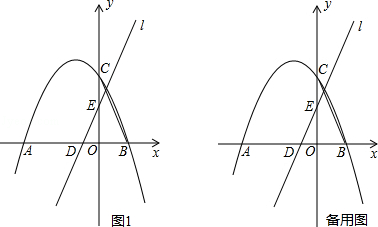
(1)求抛物线的函数解析式;
(2)若直线l:y= ![]() x+m从点C开始沿y轴向下平移,分别交x轴、y轴于点D、E.
x+m从点C开始沿y轴向下平移,分别交x轴、y轴于点D、E.
①当m>0时,在线段AC上否存在点P,使得点P,D,E构成等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
②以动直线l为对称轴,线段AC关于直线l的对称线段A′C′与二次函数图象有交点,请直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 为线段
为线段![]() 上一动点,分别过点
上一动点,分别过点![]() 作
作![]() ,
,![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的值;
的值;
(2)探究:当点![]() 满足什么条件时,
满足什么条件时,![]() 的值最小?最小值是多少?
的值最小?最小值是多少?
(3)根据(2)中的结论,请构造图形求代数式![]() 的最小值.
的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com