
科目: 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
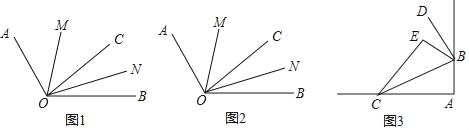
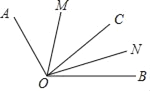
如图1,在∠AOB的内部有一条射线OC把∠AOB分成两个角,射线OM、ON分别平分∠AOC、∠BOC,试探究∠MON与∠AOB之间的数量关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论:
①请你在下表中填上当∠AOB为60°、90°、120°时∠MON的大小:
∠AOB的度数 | 60° | 90° | 120° |
∠MON的度数 |
|
|
|
②探索发现:无论∠AOB的度数是多少,∠MON与∠AOB的数量关系是不变的,请你直接写出结论:
∠MON ∠AOB.
(2)特例启发,解答题目:
如图2,如果∠AOB=α,请你求∠MON的大小(用α表示).
(3)拓展结论,设计新题:
如图3,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,求∠CBD的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,点C在线段AB上,且AC=6cm,BC=14cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长度;
(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜测出MN的长度吗?请说出你发现的结论,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
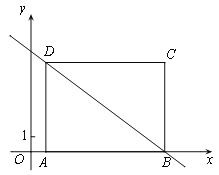
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AD=6,A(1,0), B(9,0),直线y=kx+b经过B、D两点.
(1)求直线y=kx+b的表达式;
(2)将直线y=kx+b平移,当它与矩形没有公共点时,直接写出b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
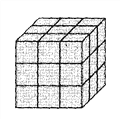
【题目】将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:
(1)其中三面涂色的小正方体有________个,两面涂色的小正方体有______个,各面都没有涂色的小正方体有________个;
(2)如果将这个正方体的棱n等分,所得的小正方体中三面涂色的有_________个,各面都没有涂色的有________个;
(3)如果要得到各面都没有涂色的小正方体125个, 那么应该将此正方体的棱______等分.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣6,0),B(2,0),C(0,﹣6).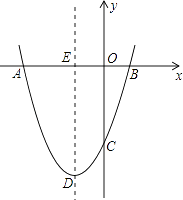
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.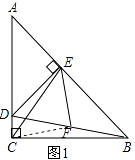
(1)若AD=3 ![]() ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE= ![]() EF;
EF;
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】小刚与小亮一起玩一种转盘游戏,图是两个完全相同的转盘,每个转盘分成面积相等的三个区域,分别用“1”,“2”,“3”表示.固定指针,同时转动两个转盘,任其自由停止. 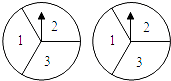
(1)用树状图或者列表法表示所有可能的结果;
(2)求两指针指的数字之和等于4的概率;
(3)若两指针指的数字都是奇数,则小刚获胜;否则,小亮获胜.游戏公平吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
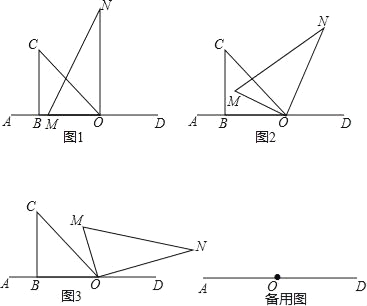
【题目】将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com