
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E. 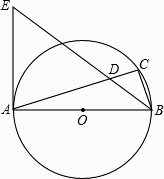
(1)∠ACB=°,理由是:;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.
查看答案和解析>>
科目: 来源: 题型:
【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目: 来源: 题型:
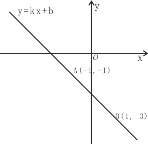
【题目】已知一次函数y=kx+b的图象经过点A(1,1)和点B(1,3).求:
(1)求一次函数的表达式;
(2)求直线AB与坐标轴围成的三角形的面积;
(3)请在x轴上找到一点P,使得PA+PB最小,并求出P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,2秒后,两点相距16个单位长度,已知点B的速度是点A的速度的3倍,(速度单位:单位长度/秒)
![]()
(1)求出点A、B运动的速度,并在数轴上标出A、B两点从原点出发运动2秒时的位置;
(2)若A、B两点从(1)中标出的位置开始,仍以原来的速度同时沿数轴向左运动,第t秒后,
①点A在数轴上的位置表示的数为 ;点B在数轴上的位置表示的数为 ;(用含t的代数式表示)
②当t为多少时,点A、B之间相距4个单位长度?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2). 
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求经过点C的反比例函数的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红的年龄的![]() 还多1岁.
还多1岁.
(1)请用含m的式子表示这三人的年龄和;
(2)若这三人的年龄和为35岁,请你求出这三人的年龄.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
(1)如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D______(A,B)的好点,但点D______(B,A)的好点.(请在横线上填是或不是)知识运用:
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为-2.数______所表示的点是(M,N)的好点;
(3)如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过______秒时,P、A和B中恰有一个点为其余两点的好点?
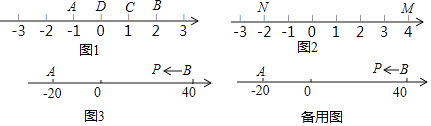
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数: ![]() ,称为数列
,称为数列![]() .计算
.计算![]() ,
, ![]() ,
, ![]() 将这三个数的最小值称为数列
将这三个数的最小值称为数列![]() 的价值.例如,对于数列2,﹣1,3,因为
的价值.例如,对于数列2,﹣1,3,因为![]() ,
, ![]() ,
, ![]() ,所以数列2,﹣1,3的价值为
,所以数列2,﹣1,3的价值为![]() .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列﹣1,2,3的价值为![]() ;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列﹣4,﹣3,2的价值为 ;
(2)将“﹣4,﹣3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为 ,取得价值最小值的数列为 (写出一个即可);
(3)将2,﹣9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com