
科目: 来源: 题型:
【题目】如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
①DE=DF;
②∠EDF=90°;
③四边形CEDF不可能为正方形;
④四边形CEDF的面积保持不变.
一定成立的结论有(把你认为正确的序号都填上)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为 . 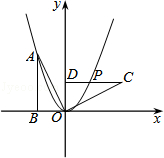
查看答案和解析>>
科目: 来源: 题型:
【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,AB∥CD,点P为定点,E、F分别是AB、CD上的动点.
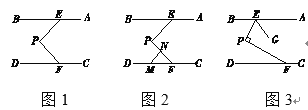
(1)求证:∠P=∠BEP+∠PFD;
(2)若点M为CD上一点,如图2,∠FMN=∠BEP,且MN交PF于N.试说明∠EPF与∠PNM的数量关系,并证明你的结论;
(3)移动E、F使得∠EPF=90°,如图3,作∠PEG=∠BEP,求∠AEG与∠PFD度数的比值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下图为人民公园中的荷花池,现要测量此荷花池两旁A、B两棵树间的距离(我们不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案.
要求:(1)画出你设计的测量平面图;
(2)简述测量方法,并写出测量的数据(长度用![]() …表示;角度用
…表示;角度用![]() …表示);
…表示);
(3)根据你测量的数据,计算A、B两棵树间的距离.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论: ①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0; 其中正确的结论有( )
A.1 个
B.2 个
C.3 个
D.4 个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2+bx+4与x轴相交于A,B两点,与y轴相交于点C,若已知B点的坐标为B(8,0)
x2+bx+4与x轴相交于A,B两点,与y轴相交于点C,若已知B点的坐标为B(8,0)
(1)求抛物线的解析式及其对称轴.
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由.
(3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;
(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、M两点之间和B、O两点之间上运动时(点P与点A、B、O三点不重合),请你分别直接写出∠CPD、∠α、∠β之间的数量关系.
 ,图1)
,图1)  ,图2)
,图2)
 ,图3)
,图3)  ,备用图)
,备用图)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F. 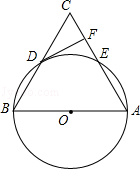
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求 ![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com