A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确

经预算，企业最多支出89万元购买设备，且要求月处理污水能力不低于1380吨．
（1）该企业有几种购买方案？
（2）哪种方案更省钱，说明理由．

【题目】林城市对教师试卷讲评课中学生参与的深度和广度进行评价，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制了如图两幅不完整的统计图，请根据图中所给信息解答下列问题：
（1）在这次评价中，一共抽查了名学生；
（2）请将条形统计图补充完整；
（3）如果全市有16万名初中学生，那么在试卷讲评课中，“独立思考”的学生约有多少万人？

【题目】若点P1（﹣1，m），P2（﹣2，n）在反比例函数y= （k＞0）的图像上，则mn（填“＞”“＜”或“=”号）．

【题目】在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN=90°．

（1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；
（2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°＜α＜45°）．
①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；
②如图2，在旋转过程中，当∠DOM=15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；
③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD=3BP时，猜想此时PE与PF的数量关系，并给出证明；当BD=mBP时，请直接写出PE与PF的数量关系．

【题目】课外兴趣小组活动时，老师出示了如下问题：如图①，已知在四边形ABCD中，AC平分∠DAB，∠DAB＝60°，∠B与∠D互补，求证：AB＋AD＝AC.

小敏反复探索，不得其解．她想，可先将四边形ABCD特殊化，再进一步解决该问题．

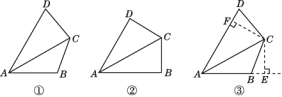
(1)由特殊情况入手，添加条件：“∠B＝∠D”，如图②，可证AB＋AD＝AC.请你完成此证明．

(2)受到(1)的启发，在原问题中，添加辅助线：过C点分别作AB，AD的垂线，垂足分别为点E，F，如图③.请你补全证明过程．

（1）数轴上表示4和1的两点之间的距离是　 　；表示﹣3和2两点之间的距离是　 　；一般地，数轴上表示数m和数n的两点之间的距离等于|m﹣n|．如果表示数a和﹣2的两点之间的距离是3，那么a＝　 　；

（2）若数轴上表示数a的点位于﹣4与2之间，求|a+4|+|a﹣2|的值；

（3）当a取何值时，|a+5|+|a﹣1|+|a﹣4|的值最小，最小值是多少？请说明理由．

【题目】如图，抛物线C1：y=x2+bx+c经过原点，与x轴的另一个交点为（2，0），将抛物线C1向右平移m（m＞0）个单位得到抛物线C2 ， C2交x轴于A，B两点（点A在点B的左边），交y轴于点C．

（1）求抛物线C1的解析式及顶点坐标；
（2）以AC为斜边向上作等腰直角三角形ACD，当点D落在抛物线C2的对称轴上时，求抛物线C2的解析式；
（3）若抛物线C2的对称轴存在点P，使△PAC为等边三角形，求m的值．

【题目】如图，分别是吊车在吊一物品时的示意图，已知吊车底盘CD的高度为2米，支架BC的长为4米，且与地面成30°角，吊绳AB与支架BC的夹角为75°，吊臂AC与地面成75°角．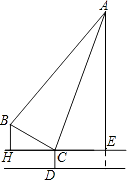
（1）求证：AB=AC
（2）求吊车的吊臂顶端A点距地面的高度是多少米？（保留根号）

【题目】在学习代数式的值时，介绍了计算程序中的框图：用“”表示数据输入、输出框；用“”表示数据处理和运算框；用“”表示数据判断框（根据条件决定执行两条路径中的某一条）.按图所示的程序计算（输入的为正整数）.

例如：输入，结果依次为、、、、，即运算循环次(第次计算结果为)结束.

（1）输入，结果依次为、___________________、、、、、.

（依次填入循环计算所缺的几次结果）

（2）输入，运算循环__________次结束.

（3）输入正整数，经过次运算结束，试求的值.