
科目: 来源: 题型:
【题目】已知△ABC中,AB=AC,∠BAC=90°.
(1)如图,若CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论
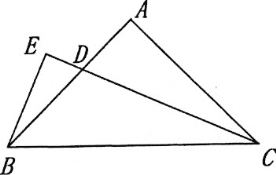
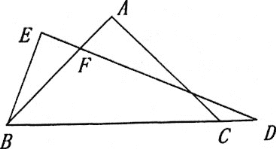
(2)如图,若点D在线段BC延长上,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE和FD的数量关系,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是菱形,点D的坐标是(0, ![]() ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.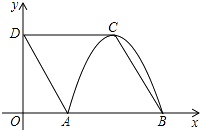
(1)求A,B,C三点的坐标;
(2)求过A,B,C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位.
查看答案和解析>>
科目: 来源: 题型:
【题目】一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系: 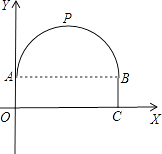
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】己知:在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.
(1)如图,若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB、AC与PB之间的数量关系,并对你的结论加以证明;

(2)如图,若∠ABC=60°-α,点P在△ABC的内部,且使∠CBP=30°,直接写出∠APC的度数________(用含α的代数式表示).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)如图,若BC=BD,求证:CD=DE;
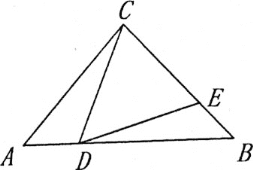
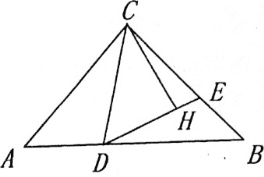
(2)如图,过点C作CH⊥DE,垂足为H,若CD=BD,![]() ,直接写出CE-BE的值为________.
,直接写出CE-BE的值为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
(1)如图,若点D为线段AC的中点,求证:AD=CE;

(2)如图,若点D为线段AC上任意一点,求证:AD=CE.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,△ABC在网格中的位置如图所示,△ABC的三个顶点都在格点上.将点A、B、C的横坐标不变,纵坐标都乘以-1,分别得到点A1、B1、C1
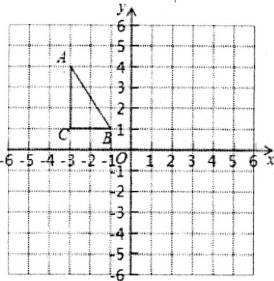
(1)写出△A1B1C1,三个顶点的坐标________;
(2)在图中画出△A1B1C1,则△ABC与△A1B1C1关于________对称;
(3)若以点A、C、P为顶点的三角形与△ABC全等,直接写出所有符合条件的点P的坐标________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com