
科目: 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别是PB、PC(靠近点P)的三等分点,△PEF、△PDC、△PAB的面积分别为S1、S2、S3 , 若AD=2,AB=2 ![]() ,∠A=60°,则S1+S2+S3的值为( )
,∠A=60°,则S1+S2+S3的值为( ) 
A.![]()
B.![]()
C.![]()
D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题:①若a<1,则(a﹣1) ![]() =﹣
=﹣ ![]() ;②平行四边形既是中心对称图形又是轴对称图形;③
;②平行四边形既是中心对称图形又是轴对称图形;③ ![]() 的算术平方根是3;④如果方程ax2+2x+1=0有两个不相等的实数根,则实数a<1.其中正确的命题个数是( )
的算术平方根是3;④如果方程ax2+2x+1=0有两个不相等的实数根,则实数a<1.其中正确的命题个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC= ![]() .
.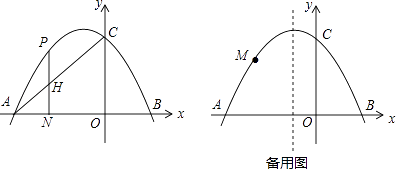
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E. 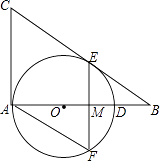
(1)若AC=5,BC=13,求⊙O的半径;
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,把横纵坐标都是整数的点称为“整点”. 
(1)直接写出函数y= ![]() 图象上的所有“整点”A1 , A2 , A3 , …的坐标;
图象上的所有“整点”A1 , A2 , A3 , …的坐标;
(2)在(1)的所有整点中任取两点,用树状图或列表法求出这两点关于原点对称的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】每年9月举行“全国中学生数学联赛”,成绩优异的选手可参加“全国中学生数学冬令营”,冬令营再选拔出50名优秀选手进入“国家集训队”.第31界冬令营已于2015年12月在江西省鹰谭一中成功举行.现将脱颖而出的50名选手分成两组进行竞赛,每组25人,成绩整理并绘制成如下的统计图:

请你根据以上提供的信息解答下列问题:
(1)请你将表格和条形统计图补充完整:
平均数 | 中位数 | 众数 | 方差 | |
一组 | 74 | __________ | __________ | 104 |
二组 | __________ | __________ | __________ | 72 |
(2)从本次统计数据来看,__________组比较稳定.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)观察图形:
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形_________________;
②线段AF与线段CE的数量关系是_________________;
(2)问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
(3)拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.
求证:DF=2CE.
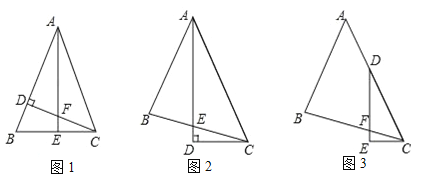
查看答案和解析>>
科目: 来源: 题型:
【题目】根据频数分布表或频数分布直方图求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权,请你依据以上知识,解决下面的实际问题.
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,并按载客量的多少分成A,B,C,D四组,得到如下统计图: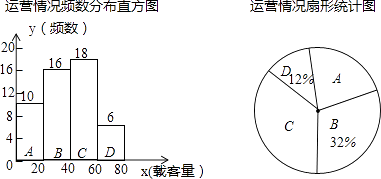
(1)求A组对应扇形圆心角的度数,并写出这天载客量的中位数所在的组;
(2)求这天5路公共汽车平均每班的载客量;
(3)如果一个月按30天计算,请估计5路公共汽车一个月的总载客量,并把结果用科学记数法表示出来.
查看答案和解析>>
科目: 来源: 题型:
【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有________条对称轴,非正方形的长方形有________条对称轴,等边三角形有___________条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1-2和图1-3都可以看作由图1-1修改得到的,仿照类似的修改方式,请你在图1-4和图1-5中,分别修改图1-2和图1-3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;


(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com