
科目: 来源: 题型:
【题目】如图,有6个质地和大小均相同的球,每个球只标有一个数字,将标有3,4,5的三个球放入甲箱,标有5,6,7的三个球放入乙箱中. 
(1)小宇从甲箱中随机摸出一个球,则“摸出标有数字是5的球”的概率是;
(2)小宇从甲箱中,小静从乙箱中各自随机摸出一个球,若小宇所摸球上的数字比小静所摸球上的数字小于1,则称小宇“屡胜一筹”,请你用列表法(或画树状图),求小宇“屡胜一筹”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离. 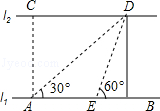
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤裁剪和拼图. 
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,BD= , 对角线MN长度的最小值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图: ①分别以B、C为圆心,以大于 ![]() BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
A.50°
B.45°
C.30°
D.25°
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A.“蒙上眼睛射击正中靶心”是必然事件
B.“抛一枚硬币,正面朝上的概率为 ![]() ”说明掷一枚质地均匀的硬币10次,必有5次正面朝上
”说明掷一枚质地均匀的硬币10次,必有5次正面朝上
C.“抛一枚均匀的正方体骰子,朝上的点数是3的概率为 ![]() ”表示随着抛掷次数的增加,“抛出朝上的点数是3”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数是3”这一事件发生的频率稳定在 ![]() 附近
附近
D.为了解某种节能灯的使用寿命,应选择全面调查
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( ) 
A.3
B.3 ![]()
C.3 ![]()
D.6
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
(1)点B的坐标为;用含t的式子表示点P的坐标为;
(2)记△OMP的面积为S,求S与t的函数关系式(0<t<6),并求当t为何值时,S有最大值?
(3)试探究:在上述运动过程中,是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC的 ![]() ?若存在,求出点T的坐标;若不存在,请说明理由.
?若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某高新企业员工的工资由基础工资、绩效工资和工龄工资三部分组成,其中工龄工资的制定充分了考虑员工对企业发展的贡献,同时提高员工的积极性,控制员工的流动率,对具有中职以上学历员工制定如下的工龄工资方案. Ⅰ.工龄工资分为社会工龄工资和企业工龄工资;
Ⅱ.社会工龄=参加本企业工作时年龄﹣18,企业工龄=现年年龄﹣参加本企业工作时年龄.
Ⅲ.当年工作时间计入当年工龄
Ⅳ.社会工龄工资y1(元/月)与社会工龄x(年)之间的函数关系式如①图所示,企业工龄工资y2(元/月)与企业工龄x(年)之间的函数关系如图②所示.
请解决以下问题
(1)求出y1、y2与工龄x之间的函数关系式;
(2)现年28岁的高级技工小张从18岁起一直实行同样工龄工资制度的外地某企业工作,为了方便照顾老人与小孩,今年小张回乡应聘到该企业,试计算第一年工龄工资每月下降多少元?
(3)已经在该企业工作超过3年的李工程师今年48岁,试求出他的工资最高每月多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN. 
(1)延长MP交CN于点E(如图2). ①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由; 
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com