【题目】小敏上午8：00从家里出发，骑车去一家超市购物，然后从这家超市返回家中．小敏离家的路程y（米）和所经过的时间x（分）之间的函数图象如图所示．请根据图象回答下列问题：

（1）小敏去超市途中的速度是多少？在超市逗留了多少时间？
（2）小敏几点几分返回到家？

【题目】计算下列各题
（1） ；
（2）解不等式：3x﹣5≤2（x+2）

【题目】实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1：2：1，用两个相同的管子在容器的5cm高度处连通（即管子底离容器底5cm），现三个容器中，只有甲中有水，水位高1cm，如图所示．若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升 cm．
（1）开始注水1分钟，丙的水位上升cm．
（2）开始注入分钟的水量后，乙的水位比甲高0.5cm．

【题目】如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠B=135°，则 的长（ ）
A.2π
B.π
C.
D.

【题目】如图，多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形，它的面积S可用公式S=a+ b﹣1（a是多边形内的格点数，b是多边形边界上的格点数）计算，这个公式称为“皮克定理”．现用一张方格纸共有200个格点，画有一个格点多边形，它的面积S=40．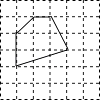

（1）这个格点多边形边界上的格点数b=（用含a的代数式表示）．
（2）设该格点多边形外的格点数为c，则c﹣a= ．

【题目】类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．

（1）概念理解：
如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．
（2）问题探究：
①小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由．
②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′，小红要使平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离（即线段BB′的长）？
（3）拓展应用：
如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD=90°，AC，BD为对角线，AC= AB，试探究BC，CD，BD的数量关系．

【题目】某企业接到一批粽子生产任务，按要求在15天内完成，约定这批粽子的出厂价为每只6元，为按时完成任务，该企业招收了新工人，设新工人李明第x天生产的粽子数量为y只，y与x满足下列关系式： y= ．

（1）李明第几天生产的粽子数量为420只？
（2）如图，设第x天每只粽子的成本是p元，p与x之间的关系可用图中的函数图象来刻画．若李明第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大，最大利润是多少元？（利润=出厂价﹣成本）
（3）设（2）小题中第m天利润达到最大值，若要使第（m+1）天的利润比第m天的利润至少多48元，则第（m+1）天每只粽子至少应提价几元？

【题目】小红将笔记本电脑水平放置在桌子上，显示屏OB与底板OA所在水平线的夹角为120°，感觉最舒适（如图1），侧面示意图为图2．使用时为了散热，她在底板下垫入散热架ACO′后，电脑转到AO′B′位置（如图3），侧面示意图为图4．已知OA=OB=24cm，O′C⊥OA于点C，O′C=12cm．
（1）求∠CAO′的度数．
（2）显示屏的顶部B′比原来升高了多少？
（3）如图4，垫入散热架后，要使显示屏O′B与水平线的夹角仍保持120°，则显示屏O′B′应绕点O′按顺时针方向旋转多少度？

【题目】如图，直线y=2x与反比例函数y= （k≠0，x＞0）的图象交于点A（1，a），B是反比例函数图象上一点，直线OB与x轴的夹角为α，tanα= ．
（1）求k的值．
（2）求点B的坐标．
（3）设点P（m，0），使△PAB的面积为2，求m的值．