
科目: 来源: 题型:
【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)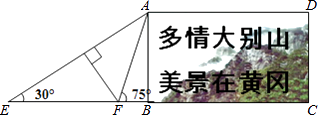
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,一次函数y=﹣2x+1与反比例函数y= ![]() 的图象有两个交点A(﹣1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,﹣2),连接DE.
的图象有两个交点A(﹣1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,﹣2),连接DE. 
(1)求k的值;
(2)求四边形AEDB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN. 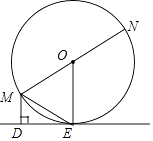
求证:
(1)DE是⊙O的切线;
(2)ME2=MDMN.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市东坡实验中学准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必选且只能选择这五项活动中的一种).
根据以上统计图提供的信息,请解答下列问题:
(1)m= , n= .
(2)补全上图中的条形统计图.
(3)若全校共有2000名学生,请求出该校约有多少名学生喜爱打乒乓球.
(4)在抽查的m名学生中,有小薇、小燕、小红、小梅等10名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这4名女生中,选取2名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母A、B、C、D代表)
查看答案和解析>>
科目: 来源: 题型:
【题目】黄麻中学为了创建全省“最美书屋”,购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元,已知学校用12000元购买的科普类图书的本数与用5000元购买的文学类图书的本数相等,求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2x+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1 , x2 , 当k=1时,求x12+x22的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在△AOB中,∠AOB=90°,AO=3cm,BO=4cm.将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段B1D=cm. 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数y= ![]() x2﹣4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为
x2﹣4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为 ![]() ,P为⊙C上一动点.
,P为⊙C上一动点.
(1)点B,C的坐标分别为B(),C();
(2)是否存在点P,使得△PBC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)连接PB,若E为PB的中点,连接OE,则OE的最大值= .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展平后,得折痕AD,BE(如图①),点O为其交点.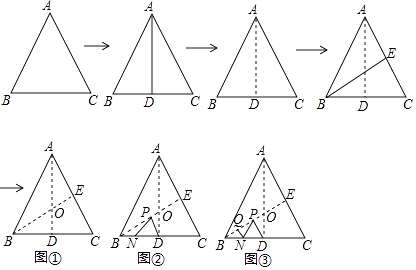
(1)探求AO到OD的数量关系,并说明理由;
(2)如图②,若P,N分别为BE,BC上的动点.
(Ⅰ)当PN+PD的长度取得最小值时,求BP的长度;
(Ⅱ)如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com