
【题目】已知:如图,在△AOB中,∠AOB=90°,AO=3cm,BO=4cm.将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段B1D=cm. 
 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,直线CD与⊙O相切于C点,AC平分∠DAB. 
(1)求证:AD⊥CD;
(2)若AD=2, ![]() ,求⊙O的半径R的长.
,求⊙O的半径R的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组 ![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(1)解不等式①,得;
(2)解不等式②,得;
(3)把不等式①和②的解集在数轴上表示出来: ![]()
(4)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线y= ![]() x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆C与x轴相切;
(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求BE:MF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC⊥BC,垂足为C,AC=4,BC=3 ![]() ,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB. 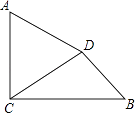
(1)线段DC=;
(2)求线段DB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y=﹣2x+1与反比例函数y= ![]() 的图象有两个交点A(﹣1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,﹣2),连接DE.
的图象有两个交点A(﹣1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,﹣2),连接DE. 
(1)求k的值;
(2)求四边形AEDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为 m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为14.4km(即MC=14.4km).在A点测得岛屿的西端点M在点A的北偏东42°方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东56°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离(结果精确到0.1km).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com