
【题目】如图,已知AB是⊙O的直径,直线CD与⊙O相切于C点,AC平分∠DAB. 
(1)求证:AD⊥CD;
(2)若AD=2, ![]() ,求⊙O的半径R的长.
,求⊙O的半径R的长.
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣x2+2bx+c与x轴交于点A、B(点A在点B的右侧),且与y轴正半轴交于点C,已知A(2,0)
(1)当B(﹣4,0)时,求抛物线的解析式;
(2)O为坐标原点,抛物线的顶点为P,当tan∠OAP=3时,求此抛物线的解析式;
(3)O为坐标原点,以A为圆心OA长为半径画⊙A,以C为圆心, ![]() OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技与经济的发展,中国廉价劳动力的优势开始逐渐消失,而作为新兴领域的机器人产业则迅速崛起,机器人自动化线的市场也越来越大,并且逐渐成为自动化生产线的主要方式,某化工厂要在规定时间内搬运1200千元化工原料.现有A,B两种机器人可供选择,已知A型机器人比B型机器人每小时多搬运30千克,A型机器人搬运900千克所用的时间与B型机器人搬运600千克所用的时间相等. 
(1)两种机器人每小时分别搬运多少化工原料?
(2)该工厂原计划同时使用这两种机器人搬运,工作一段时间后,A型机器人又有了新的搬运任务,但必须保证这批化工原料在11小时内全部搬运完毕.求:A型机器人至少工作几个小时,才能保证这批化工原料在规定的时间内完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为参加高邮市“五运会”广播操表演,准备从七、八、九三个年级分别选送到位的一男、一女共6名备选人中,每个年级随机选出1名学生,共3名学生担任领操员
(1)选出3名领操员中,男生的人数可能是
(2)求选出“两男一女”3名领操员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1 , M2 , M3 , …Mn分别为边B1B2 , B2B3 , B3B4 , …,BnBn+1的中点,△B1C1M1的面积为S1 , △B2C2M2的面积为S2 , …△BnCnMn的面积为Sn , 则Sn= . (用含n的式子表示) 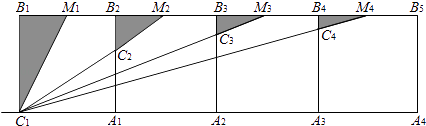
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师和学生一起去测量学校升旗台上旗杆AB的高度.如图,老师测得升旗台前斜坡FC的坡比为iFC=1:10(即EF:CE=1:10),学生小明站在离升旗台水平距离为35m(即CE=35m)处的C点,测得旗杆顶端B的仰角为α.已知tanα= ![]() ,升旗台高AF=1m,小明身高CD=1.6m,请帮小明计算出旗杆AB的高度.
,升旗台高AF=1m,小明身高CD=1.6m,请帮小明计算出旗杆AB的高度.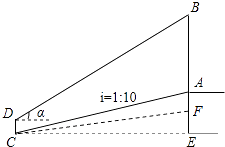
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴、y轴上,反比例函数y= ![]() (x>0)的图像经过点D,且与边BC交于点E,则点E的坐标为.
(x>0)的图像经过点D,且与边BC交于点E,则点E的坐标为. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是 ![]() ,则矩形ABCD的面积是( )
,则矩形ABCD的面积是( )
A.![]()
B.5
C.6
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△AOB中,∠AOB=90°,AO=3cm,BO=4cm.将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段B1D=cm. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com