
【题目】在平面直角坐标系中,抛物线y=﹣x2+2bx+c与x轴交于点A、B(点A在点B的右侧),且与y轴正半轴交于点C,已知A(2,0)
(1)当B(﹣4,0)时,求抛物线的解析式;
(2)O为坐标原点,抛物线的顶点为P,当tan∠OAP=3时,求此抛物线的解析式;
(3)O为坐标原点,以A为圆心OA长为半径画⊙A,以C为圆心, ![]() OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式. 
【答案】
(1)解:把点A(2,0)、B(﹣4,0)的坐标代入y=﹣x2+2bx+c得, ![]() ,
,
∴b=﹣1.c=8,
∴抛物线的解析式为y=﹣x2﹣2x+8;
(2)解:如图1,
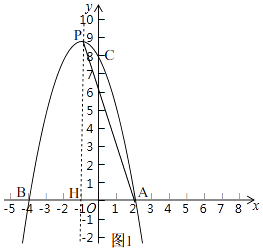
设抛物线的对称轴与x轴的交点为H,把点A(2,0)的坐标代入y=﹣x2+2bx+c得,
﹣4+4b+c=0①,
∵抛物线的顶点为P,
∴y=﹣x2+2bx+c=﹣(x﹣b)2+b2+c,
∴P(b,b2+c),
∴PH=b2+c,AH=2﹣b,
在Rt△PHA中,tan∠OAP= ![]() ,
,
∴ ![]() =3②,
=3②,
联立①②得,  ,
,
∴ ![]() (不符合题意,舍)或
(不符合题意,舍)或 ![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+8;
(3)解:∵如图2,
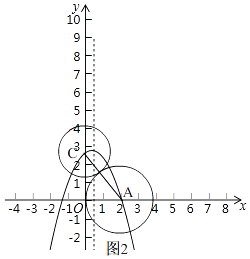
抛物线y=﹣x2+2bx+c与y轴正半轴交于点C,
∴C(0,c)(c>0),
∴ ![]() OC=
OC= ![]() c,
c,
∵A(2,0),
∴OA=2,
∴AC= ![]() ,
,
∵⊙A与⊙C外切,
∴AC= ![]() c+2=
c+2= ![]() ,
,
∴c=0(舍)或c= ![]() ,
,
把点A(2,0)的坐标代入y=﹣x2+2bx+c得,﹣4+4b+c=0,
∴b= ![]() ,
,
∴抛物线的解析式为y=﹣x2+ ![]() x+
x+ ![]() .
.
【解析】(1)利用待定系数法即可确定出函数解析式;(2)用tan∠OAP=3建立一个b,c的关系,再结合点A得出的等式即可求出b,c进而得出函数关系式;(3)用两圆外切,半径之和等于AC建立方程结合点A代入建立的方程即可得出抛物线解析式.


科目:初中数学 来源: 题型:
【题目】如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE. 
(1)若AD=DB,OC=5,求切线AC的长;
(2)求证:ED是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.
(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米,请你求出E点离地面FB的高度.
(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).
备用数据:tan60°=1.732,tan30°=0.577, ![]() =1.732,
=1.732, ![]() =1.414.
=1.414.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA= ![]() ,反比例函数y=
,反比例函数y= ![]() (k>0)的图象过CD的中点E.
(k>0)的图象过CD的中点E.
(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,是判断点G是否在反比例函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B= . 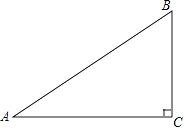
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处.
(1)求该海轮从A处到B处的航行过程中与小岛C之间的最短距离(记过保留根号);
(2)如果该海轮以每小时20海里的速度从B处沿BC方向行驶,求它从B处到达小岛C的航行时间(结果精确到0.1小时).(参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡AP的坡脚A处竖有一根电线杆AB,为固定电线杆在地面C处和坡面D处各装一根等长的引拉线BC和BD,过点D作地面MN的垂线DH,H为垂足,已知点C、A、H在一直线上,若测得AC=7米,AD=12米,坡角为30° , 试求电线杆AB的高度;(精确到0.1米)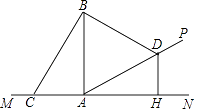
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,直线CD与⊙O相切于C点,AC平分∠DAB. 
(1)求证:AD⊥CD;
(2)若AD=2, ![]() ,求⊙O的半径R的长.
,求⊙O的半径R的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com