(1)这个梯子的顶端距地面有多高？

(2)如果梯子的顶端下滑了0.4米到A′，那么梯子的底端在水平方向滑动了几米？

（1）请画出△ABC，并写出点A、B、C的坐标；

（2）求出△AOA1的面积．

【题目】如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°，则∠EBC等于（ ）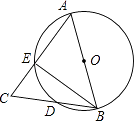
A.22.5°
B.23°
C.25°
D.30°

【题目】如图，在平面直角坐标系中，Rt△ABC的顶点B在原点O，直角边BC在x轴的正半轴上，∠ACB=90°，点A的坐标为（3， ），点D是BC边上一个动点（不与点B，C重合），过点D作DE⊥BC交AB边于点E，将∠ABC沿直线DE翻折，点B落在x轴上的点F处当△AEF为直角三角形时，点F的坐标是 ．

【题目】点A、B在数轴上分别表示实数、，A、B两点之间的距离记作AB.

当A、B两点中有一点为原点时，不妨设A点在原点.如图①所示，则AB＝OB＝＝．

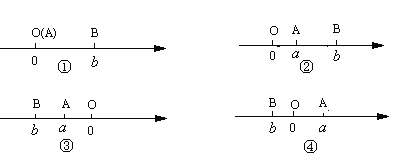
　当A、B两点都不在原点时：

(1)如图②所示，点A、B都在原点的右边，不妨设点A在点B的左侧，则AB＝OB－OA＝＝＝＝

(2)如图③所示，点A、B都在原点的左边，不妨设点A在点B的右侧，则AB＝OB－OA＝＝＝＝

(3)如图④所示，点A、B分别在原点的两边，不妨设点A在点O的右侧，则AB＝OB＋OA＝＝＝

回答下列问题：

(1)综上所述，数轴上A、B两点之间的距离AB＝　 ．

(2)数轴上表示2和－4的两点A和B之间的距离AB＝　　 　 ．

(3)数轴上表示和－2的两点A和B之间的距离AB＝　 　　 ，如果AB＝2，则的值为　　　　．

(4)若代数式有最小值，则最小值为 ．

【题目】如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于点D，P是 上的一个动点，连接AP，则AP的最小值是 ．

(1)直接写出a,b, |AB|的值. a= ，b = ， |AB|= ；

(2)设点P在数轴上对应的数为x，当|PA|-|PB|=2时，求x的值；

(3)若点P在点A的左侧，M、N分别是PA、PB的中点.当点P在点A的左侧移动时，式子|PN|-|PM|的值是否发生改变？若不变，请求出其值；若发生变化，请说明理由.

（1）小明坐该的士走了x千米的路程，应该付费多少元？

（2）小芳坐该的士走了18千米的路程，应该付费多少元？

理由如下：∵AD⊥BC于D，EG⊥BC于G，（_______）

∴∠ADC＝∠EGC＝90°，（垂直的定义），

∴AD∥EG，（_______）

∴∠1＝∠2，（_______）

∠E＝∠3，（_______）

又∵∠E＝∠1（已知），

∴______＝_______，（______）

∴AD平分∠BAC．（_______）

A. B. C. D.