
科目: 来源: 题型:
【题目】一个三角板(含30°、60°角)和一把直尺摆放位置如图所示,直尺与三角板的一角相交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF的大小为°.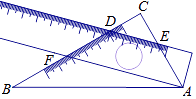
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了加强训练学生的篮球和足球运球技能,准备购买一批篮球和足球用于训练,已知1个篮球和2个足球共需116元;2个篮球和3个足球共需204元
![]() 求购买1个篮球和1个足球各需多少元?
求购买1个篮球和1个足球各需多少元?
![]() 若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
查看答案和解析>>
科目: 来源: 题型:
【题目】某班将举行知识竞赛活动,班长安排小明购买奖品.小明去文化用品店买了两种大小不同的笔记本一共a本,其中大笔记本单价8元,小笔记本单价5元.若设买单价5元小笔记本买了x本.
(1)填写下表:
单价(元/本) | 数量(本) | 金额(元) | |
小笔记本 | 5 | x | 5x |
大笔记本 | 8 |
(2)列式表示:小明买大小笔记本共花 元.
(3)若小明从班长那里拿了300元,买了40本大小不同的两种笔记本(a=40),还找回55元给班长,那么小明买了大小笔记本各多少本?
(4)若这个班下次活动中,让小明刚好花400元购买这两种大小笔记本,并且购买的小笔记本数量x要小于60本,但还要超过30本(30<x<60),请列举小明有可能购买的方案,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE
![]()
(1)若AB=18,BC=21,求DE的长;
(2)若AB=a,求DE的长;(用含a的代数式表示)
(3)若图中所有线段的长度之和是线段AD长度的7倍,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,且BD=DC,E是BC延长线上一点,且点C在AE的垂直平分线上.有下列结论:
①AB=AC=CE;②AB+BD=DE;③AD=![]() AE;④BD=DC=CE.
AE;④BD=DC=CE.
其中,正确的结论是( )

A. 只有![]() B. 只有
B. 只有![]()
C. 只有![]() D. 只有
D. 只有![]()
查看答案和解析>>
科目: 来源: 题型:
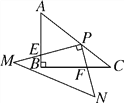
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:若两个有理数a,b满足a+b=ab,则称a,b互为特征数.
(1)3与 互为特征数;
(2)正整数n (n>1)的特征数为 ;(用含n的式子表示)
(3)若m,n互为特征数,且m+mn=-2,n+mn=3,求m+n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】直接写出结果:(1)-1+1=_____;(2)3-7=_____;
(3)4÷![]() =_____;(4)-7×0.5=_____;(5)(-2)3=_____;
=_____;(4)-7×0.5=_____;(5)(-2)3=_____;
(6)(-1)2n=_______(n为正整数);(7)4x=0的解是_____;
(8)![]() x=4 的解是_____.
x=4 的解是_____.
查看答案和解析>>
科目: 来源: 题型:
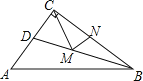
【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com