(1)如果根据三项测试的平均成绩，谁将被录用，说明理由；

(2)根据实际需要，学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩，谁将被录用，说明理由．

（思考题）如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙C的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么点B将向外移动多少米？

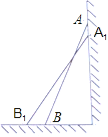
（1）请你将小明对“思考题”的解答补充完整：

解：设点B将向外移动x米，即BB1=x，

则B1C=x+0.7，A1C=AC﹣AA1=

而A1B1=2.5，在Rt△A1B1C中，由得方程 ，

解方程得x1= ，x2= ，

∴点B将向外移动 米。

（2）解完“思考题”后，小聪提出了如下两个问题：

（问题一）在“思考题”中，将“下滑0.4米”改为“下滑0.9米”，那么该题的答案会是0.9米吗？为什么？

（问题二）在“思考题”中，梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？为什么？

请你解答小聪提出的这两个问题。

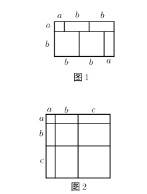
【题目】如图1，小明用1张边长为的正方形，2张边长为的正方形，3张边长分别为的长方形纸片拼成一个长为，宽为的长方形，它的面积为，于是，我们可以得到等式

请解答下列问题：

（1）根据图2，写出一个代数恒等式；

（2）利用（1）中所得的结论，解决下面的问题：已知，求的值．

（3）小明又用4张边长为的正方形，3张边长为的正方形，8张边长分别为的长方形纸片拼出一个长方形，那么该长方形的长为__________，宽为__________；

请你根据以上统计图中的信息，解答下列问题：

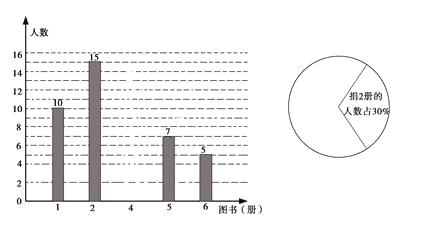
（1）该班有学生多少人？

（2）补全条形统计图；

（3）七（1）班全体同学所捐献图书的中位数和众数分别是多少？

（1）该车间应安排几天加工童装,几天加工成人装，才能如期完成任务？

（2）若加工童装一件可获利80元, 加工成人装一件可获利120元, 那么该车间加工完这批服装后，共可获利多少元？

【题目】如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y= （m≠0）的图象交于二、四象限内的A、B两点，与x轴交于C点，点B的坐标为（12，n）
， OA=10，E为x轴负半轴上一点，且tan∠AOE= ．

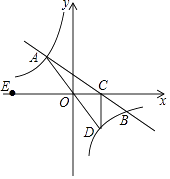
（1）求该反比例函数和一次函数的解析式；
（2）延长AO交双曲线于点D，连接CD，求△ACD的面积．

探究：（1）如图1，四边形ABCD中，AB＝BC，AD＝DC，求证：四边形ABCD是筝形；

（2）下列关于筝形的性质表述正确的是 ；（把你认为正确的序号填在横线上）

①筝形的对角线互相垂直平分； ②筝形中至少有一对对角相等；

③筝形是轴对称图形； ④筝形的面积等于两条对角线长的积的一半．

应用：

（3）如图2，在筝形ABCD中，AB≠AD，若∠ABC＝60°，∠ADC＝30°，AD＝4，请求出对角线BD的长．

小明想到一种方法，但是没有解答完：

如图2，过P作PE∥AB，∴∠APE＋∠PAB＝180°.

∴∠APE＝180°－∠PAB＝180°－130°＝50°.

∵AB∥CD.∴PE∥CD.

…………

请你帮助小明完成剩余的解答.

（2）问题迁移：请你依据小明的思路，解答下面的问题：

如图3，AD∥BC，点P在射线OM上运动，∠MDP＝∠α，∠BCP＝∠β.

①当点P在A、B两点之间时，∠CPD，∠α，∠β之间有何数量关系？请说明理由.

②当点P在A、B两点外侧时（点P与点O不重合），请直接写出∠CPD，∠α，∠β之间的数量关系.

（1）请在图中画出乙的射靶成绩的折线图；

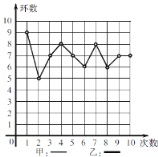
（2） 请从下列两个不同角度对这次测试结果进行分析．

①从平均数和方差相结合看（分析谁的成绩稳定些）；

②从平均数和中位数相结合看（分析谁的成绩好些）．

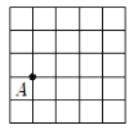
（1）已知点A在格点（即小正方形的顶点）上，画一条线段AB，长度为，且点B在格点上.

（2）以上题所画的线段AB为一边，另外两条边长分别为，. 画一个△ABC，使点C在格点上（只需画出符合条件的一个三角形）.

（3）所画出的△ABC的边AB上的高线长为 .（直接写出答案）