
【题目】(1)同题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.
小明想到一种方法,但是没有解答完:
如图2,过P作PE∥AB,∴∠APE+∠PAB=180°.
∴∠APE=180°-∠PAB=180°-130°=50°.
∵AB∥CD.∴PE∥CD.
…………
请你帮助小明完成剩余的解答.
(2)问题迁移:请你依据小明的思路,解答下面的问题:
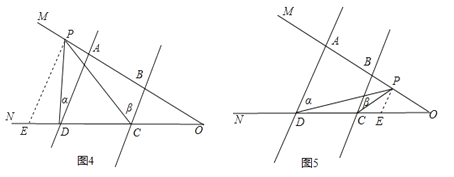
如图3,AD∥BC,点P在射线OM上运动,∠MDP=∠α,∠BCP=∠β.
①当点P在A、B两点之间时,∠CPD,∠α,∠β之间有何数量关系?请说明理由.
②当点P在A、B两点外侧时(点P与点O不重合),请直接写出∠CPD,∠α,∠β之间的数量关系.

【答案】(1)110°;(2) 详见解析
【解析】(1)根据平行线的判定与性质补充即可;
(2)①过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;
②画出图形(分两种情况(i)点P在BA的延长线上,(ii)点P在AB的延长线上),根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.
(1)剩余过程:∴∠CPE+∠PCD=1800,
∴∠CPE=1800—1200=600,∴∠APC=500+600=1100.
(2)①∠CPD=∠α+∠β.理由如下:
过P作PQ∥AD .
∵AD∥BC,∴PQ∥BC ,∴![]() ,
,
同理,![]() ,
,
∴![]() ;
;
②(i)当P在BA延长线时,如图4,过P作PE∥AD交CD于E,同①可知:∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠β﹣∠α;
(ii)当P在AB延长线时,如图5, 同①可知:∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠α﹣∠β.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,点E、F分别在边AB、边BC上,DE⊥AF,DE与AF交于点O,将线段AE沿AF进行平移至FG,过点G作GH⊥AB的延长线于点H.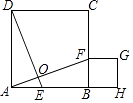
(1)判断四边形BFGH的形状并证明;
(2)写出图中所有面积相等的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点A,B的坐标分别是(a,0),(b,0)且![]() .
.
(1)求点A,B的坐标;
(2)在y轴上是否存在点C,使△ABC的面积是15?若存在,求出点C的坐标;若不存在,请说明理由.
(3)已知点P是y轴负半轴上一点,且到x轴的距离为3,若点P沿x轴负半轴方向以每秒2个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为18个平方单位?求此时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小明用1张边长为![]() 的正方形,2张边长
的正方形,2张边长![]() 为的正方形,3张边长分别为
为的正方形,3张边长分别为![]() 的长方形纸片拼成一个长为
的长方形纸片拼成一个长为![]() ,宽为
,宽为![]() 的长方形,它的面积为
的长方形,它的面积为![]() ,于是,我们可以得到等式
,于是,我们可以得到等式![]()
请解答下列问题:
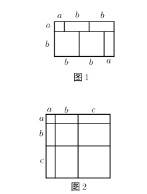
(1)根据图2,写出一个代数恒等式;
(2)利用(1)中所得的结论,解决下面的问题:已知![]() ,求
,求![]() 的值.
的值.
(3)小明又用4张边长为![]() 的正方形,3张边长为
的正方形,3张边长为![]() 的正方形,8张边长分别为
的正方形,8张边长分别为![]() 的长方形纸片拼出一个长方形,那么该长方形的长为__________,宽为__________;
的长方形纸片拼出一个长方形,那么该长方形的长为__________,宽为__________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
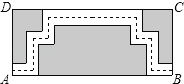
A.100米 B.99米 C.98米 D.74米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于点E,连接AD,则下列结论正确的个数是( )
①AD⊥BC;②∠EDA=∠B;③OA= ![]() AC;④DE是⊙O的切线.
AC;④DE是⊙O的切线.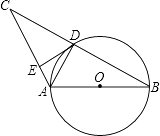
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
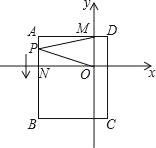
【题目】如图,平面直角坐标系中,ABCD为长方形,其中点A、C坐标分别为(﹣8,4)、(2,﹣8),且AD∥x轴,交y轴于M点,AB交x轴于N.
(1)求B、D两点坐标和长方形ABCD的面积;
(2)一动点P从A出发(不与A点重合),以![]() 个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
个单位/秒的速度沿AB向B点运动,在P点运动过程中,连接MP、OP,请直接写出∠AMP、∠MPO、∠PON之间的数量关系;
(3)是否存在某一时刻t,使三角形AMP的面积等于长方形面积的![]() ?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
?若存在,求t的值并求此时点P的坐标;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com