A. 1︰1︰1

B. 1︰2︰3

C. 2︰3︰4

D. 3︰4︰5

【题目】如图所示，在ABCD中，对角线AC与BD相交于点O，过点O作一条直线分别交AB，CD于点E，F．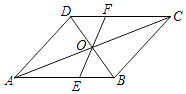
（1）求证：OE=OF；
（2）若AB=6，BC=5，OE=2，求四边形BCFE的周长．

【题目】一张宽为6cm的平行四边形纸带ABCD如图1所示，AB=10cm，小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴（要求包贴时没有重叠部分）．小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析．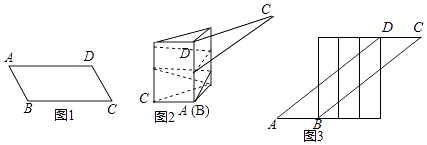

（1）若纸带在侧面缠绕三圈，正好将这个直三棱柱纸盒的侧面全部包贴满．则纸带AD的长度为 cm；
（2）若AD=100cm，纸带在侧面缠绕多圈，正好将这个直三棱柱纸盒的侧面全部包贴满．则这个直三棱柱纸盒的高度是 cm．

对数的创始人是苏格兰数学家纳皮尔（J．Nplcr，1550﹣1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evlcr，1707﹣1783年）才发现指数与对数之间的联系．

对数的定义：一般地，若ax=N（a＞0，a≠1），那么x叫做以a为底N的对数，记作：x=logaN．比如指数式24=16可以转化为4=log216，对数式2=log525可以转化为52=25．

我们根据对数的定义可得到对数的一个性质：loga（MN）=logaM+logaN（a＞0，a≠1，M＞0，N＞0）；理由如下：

设logaM=m，logaN=n，则M=am，N=an

∴MN=aman=am+n，由对数的定义得m+n=loga（MN）

又∵m+n=logaM+logaN

∴loga（MN）=logaM+logaN

解决以下问题：

（1）将指数43=64转化为对数式_____；

（2）证明loga=logaM﹣logaN（a＞0，a≠1，M＞0，N＞0）

（3）拓展运用：计算log32+log36﹣log34=_____．

【题目】如图，在⊙O中，AB是直径，CD是弦，AB⊥CD，垂足为E，连接CO，AD，∠BAD=20°，则下列说法中正确的是（ ）

A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD

【题目】某学校在进行防溺水安全教育活动中，将以下几种在游泳时的注意事项写在纸条上并折好，内容分别是：①互相关心；②互相提醒；③不要相互嬉水；④相互比潜水深度；⑤选择水流湍急的水域；⑥选择有人看护的游泳池．小颖从这6张纸条中随机抽出一张，抽到内容描述正确的纸条的概率是（ ）
A.
B.
C.
D.

A. 点F B. 点E C. 点A D. 点C

【题目】我们规定：＝（a≠0），即a的负P次幂等于a的p次幂的倒数．例：＝

（1）计算：＝__；＝__；

（2）如果＝，那么p＝__；如果＝，那么a＝__；

（3）如果＝，且a、p为整数，求满足条件的a、p的取值．

【题目】如图，已知抛物线y=-x2+bx+c与一直线相交于A（-1，0），C（2，3）两点，与y轴交于点N．其顶点为D．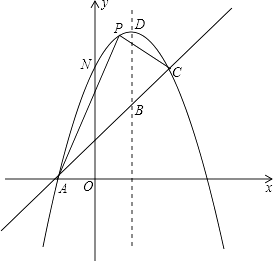

（1）抛物线及直线AC的函数关系式；
（2）设点M（3，m），求使MN+MD的值最小时m的值；
（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；
（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．

【题目】如图：三角形ABC内接于圆O，∠BAC与∠ABC的角平分线AE，BE相交于点E，延长AE交外接圆O于点D，连接BD，DC，且∠BCA=60°

（1）求∠BED的大小；
（2）证明：△BED为等边三角形；
（3）若∠ADC=30°，圆O的半径为r，求等边三角形BED的边长．