
科目: 来源: 题型:
【题目】在一个不透明的盒子中装有三张卡片,分别标有数字1,2,3,这些卡片除数字不同外其余均相同.小吉从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求两次抽取的卡片上数字之和为奇数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线l1的函数关系式为![]() ,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,
,且l1与x轴交于点D,直线l2经过定点A(4,0),B(﹣1,5),直线l1与l2相交于点C,

(1)求直线l2的解析式;
(2)求△ADC的面积;
(3)在直线l2上存在一点F(不与C重合),使得△ADF和△ADC的面积相等,请求出F点的坐标;
(4)在x轴上是否存在一点E,使得△BCE的周长最短?若存在请求出E点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
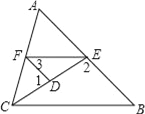
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线与x轴交于点和A(﹣1,0)和点B(4,0),与y轴交于点C(0,2).
(1)求抛物线解析式;
(2)点P是抛物线BC段上一点,PD⊥BC,PE∥y轴,分别交BC于点D、E.当DE= ![]() 时,求点P的坐标;
时,求点P的坐标;
(3)M是平面内一点,将符合(2)条件下的△PDE绕点M沿逆时针方向旋转90°后,点P,D,E的对应点分别是P′、D′、E′.设P′E′的中点为N,当抛物线同时经过D′与N时,求出D′的横坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2 016个三角形的周长为( )
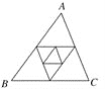
A. 22 016 B. 22 017 C. (![]() )2 016 D. (
)2 016 D. (![]() )2 015
)2 015
查看答案和解析>>
科目: 来源: 题型:
【题目】完成下面推理过程:

如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________ _________),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________ ________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°,恒成立的结论有

A. ①③⑤ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】【问题提出】如图①,已知海岛A到海岸公路BD的距离为AB,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D选在何处时,所用时间最短?
【特例分析】若n=2,则时间t= ![]() +
+ ![]() ,当a为定值时,问题转化为:在BC上确定一点D,使得AD+
,当a为定值时,问题转化为:在BC上确定一点D,使得AD+ ![]() 的值最小.如图②,过点C做射线CM,使得∠BCM=30°.
的值最小.如图②,过点C做射线CM,使得∠BCM=30°.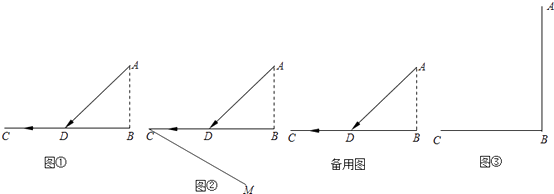
(1)过点D作DE⊥CM,垂足为E,试说明:DE= ![]() ;
;
(2)【问题解决】请在图②中画出所用时间最短的登陆点D′,并说明理由.
(3)【模型运用】请你仿照“特例分析”中的相关步骤,解决图①中的问题(写出具体方案,如相关图形呈现、图形中角所满足的条件、作图的方法等).
(4)如图③,海面上一标志A到海岸BC的距离AB=300m,BC=300m.救生员在C点处发现标志A处有人求救,
立刻前去营救,若救生员在岸上跑的速度都是6m/s,在海中游泳的速度都是2m/s,求救生员从C点出发到
达A处的最短时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com