如图，已知AB∥CD，点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以点E，F为圆心，大于EF长为半径作圆弧，两条圆弧交于点P，作射线AP，交CD于点M．

问题解决：

(1)若∠ACD=78°，求∠MAB的度数；

(2)若CN⊥AM，垂足为点N，求证：△CAN≌△CMN．

实验探究：

(3)直接写出当∠CAB的度数为多少时？△CAM分别为等边三角形和等腰直角三角形．

【题目】下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A.
B.
C.
D.

(1)t为______时，△PBQ是等边三角形？

(2)P，Q在运动过程中，△PBQ的形状不断发生变化，当t为何值时，△PBQ是直角三角形？说明理由．

【题目】甲乙两地相距72千米，李磊骑自行车往返两地一共用了7小时，已知他去时的平均速度比返回时的平均速度快，求李磊去时的平均速度是多少？

小芸同学解法如下：

解：设李磊去时的平均速度是x千米/时，则返回时的平均速度是(1-)x千米/时，由题意得：+=7，…

你认为小芸同学的解法正确吗？若正确，请写出该方程所依据的等量关系，并完成剩下的步骤；若不正确，请说明原因，并完整地求解问题．

(1)当∠AOC=30°时，如果我们通过分类讨论、画图尝试可以找到满足条件的点P共有______个．

(2)若在直线BC上有且只有两个满足条件的点P，则∠AOC=______．

A. 2B. C. 4D.

（1）∠DCA的度数；

（2）∠DCE的度数．

已知：如图，点 D，E，F 分别在线段 AB，BC，AC 上，连接 DE、EF，DM 平分∠ADE 交 EF 于点 M，∠1+∠2=180°． 求证：∠B =∠BED．

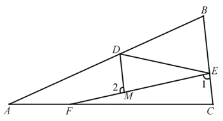
证明：∵∠1+∠2=180°（已知），

又∵∠1+∠BEM=180°（平角定义），

∴∠2=∠BEM（ ），

∴DM∥ （ ）．

∴∠ADM =∠B（ ），

∠MDE =∠BED（ ）．

又∵DM 平分∠ADE (已知)，

∴∠ADM =∠MDE (角平分线定义)．

∴∠B =∠BED（ ）．

【题目】如图已知一次函数y=﹣x+b与反比例函数y= 的图象有2个公共点，则b的取值范围是（ ）

A.b＞2
B.﹣2＜b＜2
C.b＞2或b＜﹣2
D.b＜﹣2