【题目】在平面直角坐标系中，点为轴上的动点，点为轴上方的动点，连接，，．

（1）如图1，当点在轴上，且满足的角平分线与的角平分线交于点，请直接写出的度数；

（2）如图2，当点在轴上，的角平分线与的角平分线交于点，点在的延长线上，且满足，求；

（3）如图3，当点在第一象限内，点是内一点，点，分别是线段，上一点，满足：，，．

以下结论：①；②平分；③平分；④．

正确的是：________．（请填写正确结论序号，并选择一个正确的结论证明，简写证明过程）．

【题目】在中，若存在一个内角角度，是另外一个内角角度的倍（为大于1的正整数），则称为倍角三角形．例如，在中，，，，可知，所以为3倍角三角形．

（1）在中，，，则为________倍角三角形；

（2）若是3倍角三角形，且其中一个内角的度数是另外一个内角的余角的度数的，求的最小内角．

（3）若是2倍角三角形，且，请直接写出的最小内角的取值范围．

求证：（1）AM⊥DM；

（2）M为BC的中点．

【题目】定义：在同一平面内，如果矩形ABCD的四个顶点到⊙M上一点的距离相等，那么称这个矩形ABCD是⊙M的“伴侣矩形”．如图，在平面直角坐标系xOy中，直线l：y= x﹣3交x轴于点M，⊙M的半径为2，矩形ABCD沿直线运动（BD在直线l上），BD=2，AB∥y轴，当矩形ABCD是⊙M的“伴侣矩形”时，点C的坐标为（ ）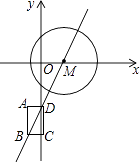

A.（ ﹣ ，﹣ ）
B.（ ﹣ ，﹣ ）
C.（ ﹣ ，﹣ ）或（ + ，﹣ ）
D.（ ﹣ ，﹣ ）或（ + ， ）

（1）求证：△ADE≌△BFE；

（2）连接EG，判断EG与DF的位置关系并说明理由．

(a)某学习小组在学习时遇到如下问题：如图①，在Rt△ABC中，∠C＝90°，D为边BC上一点，DA＝DB，E为AD延长线上一点，∠AEB＝120°，猜想BC、EA、EB的数量关系，并证明结论．大家经探究发现：过点B作BF⊥AE交AE的延长线于F，如图②所示，构造全等三角形使问题容易求解，请写出解答过程．

(b)参考上述思考问题的方法，解答下列问题：

如图③，等腰△ABC中，AB＝AC，H为AC上一点，在BC的延长线上顺次取点E、F，在CB的延长线上取点BD，使EF＝DB，过点E作EG∥AC交DH的延长线于点G，连接AF，若∠HDF+∠F＝∠BAC．

(1)探究∠BAF与∠CHG的数量关系；

(2)请在图中找出一条和线段AF相等的线段，并证明你的结论．

为了响应某市的“四个一”工程，培养学生的爱国主义情怀，某校学生和带队老师在5月下旬某天集体乘车去参观抗日战争纪念馆．已知学生的数量是带队老师的12倍多20人，学生和老师的总人数共540人．

（1）请求出去参观抗日战争纪念馆学生和老师各多少人？

（2）如果学校准备租赁型大巴车和型大巴车共14辆，（其中型大巴车最多有7辆）已知型大巴车每车最多可以载35人，日租金为2000元，其中型大巴车每车最多可以载45人，日租金为3000元请求出最经济的租赁车辆方案．

【题目】如图，Rt△ABC中，∠ACB=90°，AC=3，BC=4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E，F，则线段B′F的长为（ ）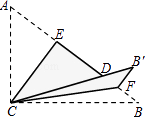

A.
B.
C.
D.

【题目】作图题：如图，在平面直角坐标系中，，，

（1）画出的边上的高CH；

（2）将平移到（点和点对应，点和点对应，点和点对应），若点的坐标为，请画出平移后的；

（3）若，为平面内一点，且满足与全等，请直接写出点的坐标．