
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过(-1,0)(0,3),下列结论中错误的是( )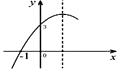
A.abc<0
B.9a+3b+c=0
C.a-b=-3
D.4ac﹣b2<0
查看答案和解析>>
科目: 来源: 题型:
【题目】工厂工人小李生产A、B两种产品.若生产A产品10件,生产B产品10件,共需时间350分钟;若生产A产品30件,生产B产品20件,共需时间850分钟.
(1)小李每生产一件![]() 种产品和每生产一件
种产品和每生产一件![]() 种产品分别需要多少分钟;
种产品分别需要多少分钟;
(2)小李每天工作8个小时,每月工作25天.如果小李四月份生产![]() 种产品
种产品![]() 件(
件(![]() 为正整数).
为正整数).
①用含![]() 的代数式直接表示小李四月份生产
的代数式直接表示小李四月份生产![]() 种产品的件数;
种产品的件数;
②已知每生产一件![]() 产品可得1.40元,每生产一件
产品可得1.40元,每生产一件![]() 种产品可得2.80元,若小李四月份的工资不少于1500元,求
种产品可得2.80元,若小李四月份的工资不少于1500元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题:
-3 -5 0 +3 +4
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,最大乘积是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小的商是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算的式子.(至少写出两种)
查看答案和解析>>
科目: 来源: 题型:
【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是____,因变量是______;
(2)小明家到滨海公园的路程为____ km,小明在中心书城逗留的时间为____ h;
(3)小明出发______小时后爸爸驾车出发;
(4)图中A点表示___________________________________;
(5)小明从中心书城到滨海公园的平均速度为______km/h,小明爸爸驾车的平均速度为______km/h;(补充;爸爸驾车经过______追上小明);
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=90°,∠BCD=135°,且AB=3cm,BC=7cm,CD=5![]() cm,点M从点A出发沿折线A﹣B﹣C﹣D运动到点D,且在AB上运动的速度为
cm,点M从点A出发沿折线A﹣B﹣C﹣D运动到点D,且在AB上运动的速度为![]() cm/s,在BC上运动的速度为1cm/s,在CD上运动的速度为
cm/s,在BC上运动的速度为1cm/s,在CD上运动的速度为![]() cm/s,连接AM、DM,当点M运动时间为_____(s)时,△ADM是直角三角形.
cm/s,连接AM、DM,当点M运动时间为_____(s)时,△ADM是直角三角形.

查看答案和解析>>
科目: 来源: 题型:
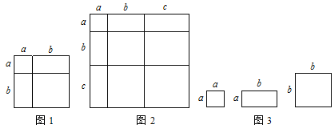
【题目】(知识生成)我们知道,用两种不同的方法计算同一个几何图形的面积,可以得到一些代数恒等式.
例如:如图可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
⑴ 根据如图,写出一个代数恒等式:
![]() ;
;
⑵ 利用⑴中得到的结论,解决下面的问题:若a+b+c=12,![]() ,
,
则![]() ;
;
⑶ 小明同学用如图中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+3b)的长方形,则x+y+z= ;
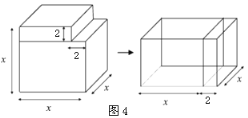
(知识迁移)⑷ 类似地,用两种不同的方法计算几何体的体积同样可以得到一些代数恒等式.如图表示的是一个边长为x的正方体挖去一个边长为2的小长方体后重新拼成一个新长方体.请你根据如图中两个图形的变化关系,写出一个代数恒等式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为(4,1)的抛物线交y轴于点A,交x轴于B,C两点(点B在点C的左侧),已知C点坐标为(6,0).
(1)求此抛物线的解析式;
(2)已知点P是抛物线上的一个动点,且位于A,C两点之间.问:当点P运动到什么位置时,△PAC的面积最大?求出△PAC的最大面积;
(3)连接AB,过点B作AB的垂线交抛物线于点D,以点C为圆心的圆与抛物线的对称轴l相切,先补全图形,再判断直线BD与⊙C的位置关系并加以证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,点D为BC边的中点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E,F,且∠EDF与∠A互补.
(1)如图1,若AB=AC,且∠A=90°,则线段DE与DF有何数量关系?请直接写出结论;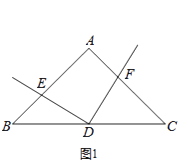
(2)如图2,若AB=AC,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请说明理由;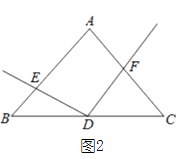
(3)如图3,若AB:AC=m:n,探索线段DE与DF的数量关系,并证明你的结论.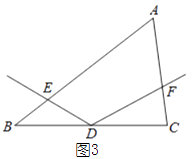
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com