
【题目】小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题:
-3 -5 0 +3 +4
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,最大乘积是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小的商是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算的式子.(至少写出两种)
【答案】(1)15;(2)![]() ;(3)取-3,-5,0,+3,四个数,
;(3)取-3,-5,0,+3,四个数,![]() ;取-3,-5,+3,+4四个数,
;取-3,-5,+3,+4四个数,![]() .
.
【解析】
(1)观察这五个数,要找乘积最大的就要找符号相同且数值最大的数,所以选-3和-5;
(2)2张卡片上数字相除的商最小就要找符号不同,且分母绝对值越小越好,分子绝对值越大越好,所以就要选3和-5,且-5为分子;
(3)从中取出4张卡片,用学过的运算方法,使结果为24,这就不唯一,用加减乘除只要答数是24即可,比如-3、-5、0、3,四个数,{0-[(-3)+(-5)]}×3=24;再如抽取-3、-5、3、+4,则-[(-3)÷3+(-5)]×4=24.
(1)(-3)×(-5)=15;
(2)(5)÷(+3)=![]() ;
;
(3)方法不唯一,如:抽取3、5、0、+3四个数,则{0[(3)+(5)]}×3=24;
如:抽取3、5、3、4,则[(3)÷3+(5)]×4=24.


科目:初中数学 来源: 题型:
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A![]() B
B![]() C
C![]() .
.
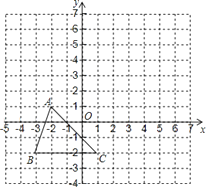
(1)在图中画出△A![]() B
B![]() C
C![]() ;
;
(2)写出点A![]() 、B
、B![]() 、C
、C![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识生成)我们知道,用两种不同的方法计算同一个几何图形的面积,可以得到一些代数恒等式.
例如:如图可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
⑴ 根据如图,写出一个代数恒等式:
![]() ;
;
⑵ 利用⑴中得到的结论,解决下面的问题:若a+b+c=12,![]() ,
,
则![]() ;
;
⑶ 小明同学用如图中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+3b)的长方形,则x+y+z= ;
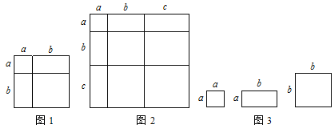
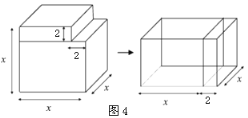
(知识迁移)⑷ 类似地,用两种不同的方法计算几何体的体积同样可以得到一些代数恒等式.如图表示的是一个边长为x的正方体挖去一个边长为2的小长方体后重新拼成一个新长方体.请你根据如图中两个图形的变化关系,写出一个代数恒等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0,
其中结论正确有( )个。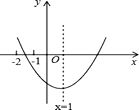
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com