
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A![]() B
B![]() C
C![]() .
.
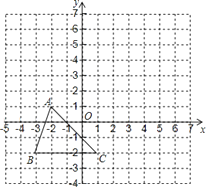
(1)在图中画出△A![]() B
B![]() C
C![]() ;
;
(2)写出点A![]() 、B
、B![]() 、C
、C![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
【答案】(1)见解析;(2)A′(0,4),B′(-1,1),C′(3,1);(3)存在,点P的坐标是(0,1)或(0,-5).
【解析】
(1)分别把A,B,C三点向上平移3个单位长度,再向右平移2个单位长度即得A′,B′,C′三点连线即可;(2)可以先写出A,B,C三点坐标,然后分别把各点的横坐标加2,纵坐标加3即得A′,B′,C′坐标;(3)先把△ABC面积求出来,S△ABC=4×3÷2=6,若存在,设P点到BC的距离为x,BC=4,当△PBC与△ABC面积相等时,4x÷2=6,x=3,P点到BC的距离为3的点有2个为±3,当为3时,P点纵坐标是3-2=1,当为-3时,P点纵坐标是-3-2=-5,综上所述,y轴上存在点P,使得△PBC与△ABC面积相等,点P的坐标是(0,1)或(0,-5).
解:(1)分别把A,B,C三点向上平移3个单位长度,再向右平移2个单位长度即得A′,B′,C′,画出三角形A′B′C′;如图:
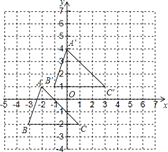
(2)由图写出A,B,C三点坐标:A(-2,1),B(-3,-2),C(1,-2),
∵上平移3个单位长度,右平移2个单位长度,
∴各点的横坐标加2,纵坐标加3得,:A′(0,4),B′(-1,1),C′(3,1).
(3)由图可知,S△ABC=4×3÷2=6,BC=4,设P点到BC的距离为x,4x÷2=6,x=3,
∵P点到BC的距离为3的点有2个为±3,
∴当为3时,P点纵坐标是3-2=1,当为-3时,P点纵坐标是-3-2=-5,P点横坐标是0,
∴点P的坐标是(0,1)或(0,-5).


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】小华和小峰是两名自行车爱好者,小华的骑行速度比小峰快![]() 两人准备在周长为250米的赛道上进行一场比赛
两人准备在周长为250米的赛道上进行一场比赛![]() 若小华在小峰出发15秒之后再出发,图中
若小华在小峰出发15秒之后再出发,图中![]() 、
、![]() 分别表示两人骑行路程与时间的关系.
分别表示两人骑行路程与时间的关系.
![]() 小峰的速度为______米
小峰的速度为______米![]() 秒,他出发______米后,小华才出发;
秒,他出发______米后,小华才出发;
![]() 小华为了能和小峰同时到达终点,设计了两个方案,方案一:加快骑行速度;方案二:比预定时间提前出发.
小华为了能和小峰同时到达终点,设计了两个方案,方案一:加快骑行速度;方案二:比预定时间提前出发.
![]() 图______
图______![]() 填“A“”或“B“
填“A“”或“B“![]() 代表方案一;
代表方案一;
![]() 若采用方案二,小华必须在小峰出发多久后开始骑行?求出此时小华骑行的路程与时间的函数关系式.
若采用方案二,小华必须在小峰出发多久后开始骑行?求出此时小华骑行的路程与时间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE.其中,正确的有( )
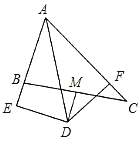
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
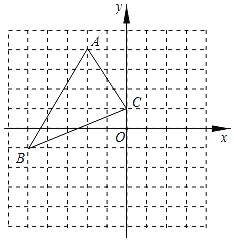
【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为A(﹣2,4),B(﹣5,﹣1),C(0,1),把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形A'B'C'.
(1)画出三角形ABC和平移后A′B′C′的图形;
(2)写出三个顶点A',B',C'的坐标;
(3)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(列二元一次方程组解应用题)某公司共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供300名员工就餐;同时开放1个大餐厅,1个小餐厅,可供170名员工就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名员工就餐;
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全体450名员工就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.

(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y= ![]() +bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( ).
+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( ).
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题:
-3 -5 0 +3 +4
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,最大乘积是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小的商是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算的式子.(至少写出两种)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com