
【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.

(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
【答案】(1)AE∥FC,理由见解析;(2)AD∥BC,理由见解析;(3)BC平分∠DBE,理由见解析.
【解析】
(1)证明∠1=∠CDB,利用同位角相等,两直线平行即可证得结论;
(2)根据平行线的性质可以证得∠A=∠CBE,然后利用平行线的判定即可证得结论;
(3)根据平行线的性质证明∠EBC=∠CBD即可证得结论.
(1)AE∥FC.
理由如下:
∵∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义),
∴∠1=∠CDB,
∴AE∥FC( 同位角相等两直线平行);
(2)AD∥BC.
理由如下:
∵AE∥CF,
∴∠C=∠CBE(两直线平行,内错角相等),
又∵∠A=∠C,
∴∠A=∠CBE,
∴AD∥BC(同位角相等,两直线平行);
(3)BC平分∠DBE.
理由如下:
∵AD平分∠BDF,
∴∠FDA=∠ADB,
∵AE∥CF,AD∥BC,
∴∠FDA=∠A=∠CBE,∠ADB=∠CBD,
∴∠EBC=∠CBD,
∴BC平分∠DBE.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系 ![]() 中,
中, ![]() 是坐标原点。已知A(0,
是坐标原点。已知A(0, ![]() ),B(1,0),C(6,
),B(1,0),C(6, ![]() ),有一抛物线恰好经过这三点.
),有一抛物线恰好经过这三点.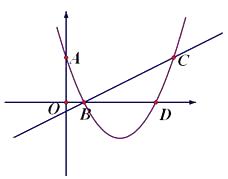
(1)求该抛物线解析式;
(2)若抛物线交 ![]() 轴的另一交点为D,那么抛物线上是否存在一点P,使得
轴的另一交点为D,那么抛物线上是否存在一点P,使得 ![]() ,若存在,求出P的坐标,若不存在,请说明理由。
,若存在,求出P的坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了出行方便,现在很多家庭都购买了小汽车.又由于能源紧张和环境保护,石油的市场价格常常波动.为了在价格的波动中尽可能减少损失,常常有两种加油方案.
方案一:每次加50元的油.方案二:每次加50升的油.
请同学们以2次加油为例(第一次油价为a元/升,第二次油价为b元/升,a>0,b>0且a≠b),计算这两种方案中,哪种加油方案更实惠便宜(平均单价小的便宜)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=1,有以下四个结论:
①abc>0;②b2-4ac>0;③b=-2a;④a+b+c>2.其中正确的是 (填写序号)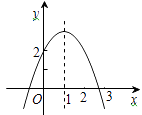
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A![]() B
B![]() C
C![]() .
.
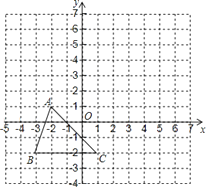
(1)在图中画出△A![]() B
B![]() C
C![]() ;
;
(2)写出点A![]() 、B
、B![]() 、C
、C![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x 2+bx+c与x轴交于A、B两点,与y轴交于点C,已知经过B、C两点的直线的表达式为y=-x+3.

(1)求抛物线的函数表达式;
(2)点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?
(3)在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组为了解同学们上学年参加社会实践活动的天数,随机抽查了该市部分八年级学生,来了解上学年参加社会实践活动的天数,并用得到的数据绘制了如图两幅不完整的统计图![]() 请你根据图中提供的信息问答下列问题:
请你根据图中提供的信息问答下列问题:
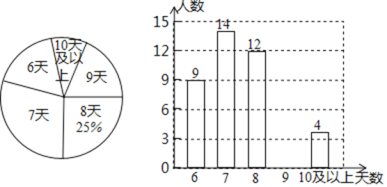
![]() 本次共抽查了多少人?
本次共抽查了多少人?
![]() 补全条形统计图.
补全条形统计图.
![]() 在这次调查中,参加社会实践活动天数的众数和中位数分别是多少?
在这次调查中,参加社会实践活动天数的众数和中位数分别是多少?
![]() 如果本区市共有八年级学生14400人,请你估计“参加社会实践活动时间不少于9天”的有多少人?
如果本区市共有八年级学生14400人,请你估计“参加社会实践活动时间不少于9天”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公司投资750万元,成功研制出一种市场需求量较大的产品,并再投入资金1750万元进行相关生产设备的改进.已知生产过程中,每件产品的成本为60元.在销售过程中发现,当销售单价定为120元时,年销售量为24万件;销售单价每增加10元,年销售量将减少1万件.设销售单价为x(元)(x>120),年销售量为y(万件),第一年年获利(年获利=年销售额﹣生产成本)为z(万元).
(1)求出y与x之间,z与x之间的函数关系式;
(2)该公司能否在第一年收回投资.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0,
其中结论正确有( )个。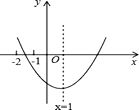
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com