
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0,
其中结论正确有( )个。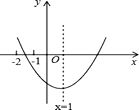
A.2个
B.3个
C.4个
D.5个
【答案】B
【解析】图象与x轴有两个交点,则 ![]() -4ac>0,则
-4ac>0,则 ![]() >4ac,∴①正确;根据图形可得:a>0,b<0,c<0,则abc>0,∴②正确;根据对称轴为x=1,即-
>4ac,∴①正确;根据图形可得:a>0,b<0,c<0,则abc>0,∴②正确;根据对称轴为x=1,即- ![]() =1,则-b=2a,则2a+b=0,∴③错误;当x=-2时,y>0,即4a-2b+c>0,根据③可得:-b=2a,则4a+4a+c>0,即8a+c>0,∴④错误;根据图象可得:当x=3和x=-1时y的值相等,当x=-1时,y>0,所以当x=3时,y>0,即9a+3b+c>0,∴⑤正确.∴①、②、⑤正确.
=1,则-b=2a,则2a+b=0,∴③错误;当x=-2时,y>0,即4a-2b+c>0,根据③可得:-b=2a,则4a+4a+c>0,即8a+c>0,∴④错误;根据图象可得:当x=3和x=-1时y的值相等,当x=-1时,y>0,所以当x=3时,y>0,即9a+3b+c>0,∴⑤正确.∴①、②、⑤正确.
答案:B
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.

(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
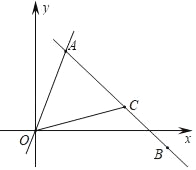
【题目】如图,直线OA与直线BC相交于点A,且点B的坐标为(5,﹣1),点C的坐标为(3,1),直线OA的解析式为y=3x
(1)求直线BC的解析式;
(2)求点A的坐标;
(3)求△OAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为BC边的中点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E,F,且∠EDF与∠A互补.
(1)如图1,若AB=AC,且∠A=90°,则线段DE与DF有何数量关系?请直接写出结论;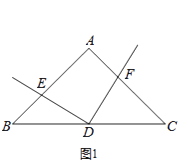
(2)如图2,若AB=AC,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请说明理由;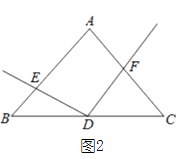
(3)如图3,若AB:AC=m:n,探索线段DE与DF的数量关系,并证明你的结论.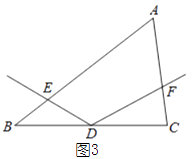
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题:
-3 -5 0 +3 +4
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,最大乘积是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小的商是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算的式子.(至少写出两种)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() .若将
.若将![]() 绕点
绕点![]() 顺时针旋转至Δ
顺时针旋转至Δ![]() ,使射线
,使射线![]() 与射线
与射线![]() 相交于点
相交于点![]() (不与
(不与![]() 、
、![]() 重合).
重合).
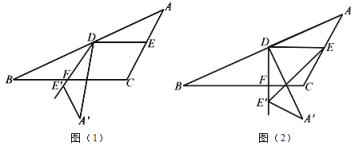
(1)如图(1),若![]() ,则
,则![]() ;
;
(2)如图(2),连结![]() ,若
,若![]() ,试求出
,试求出![]() 的度数;
的度数;
(3)请探究![]() 与
与![]() 之间所满足的数量关系,并加以证明.
之间所满足的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备购买A、B两种零件,已知A种零件的单价比B种零件的单价多30元,而用900元购买A种零件的数量和用600元购买B种零件的数量相等.
(1)求A、B两种零件的单价;
(2)根据需要,工厂准备购买A、B两种零件共200件,工厂购买两种零件的总费用不超过14700元,求工厂最多购买A种零件多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由相同大小的△按一定规律组成的,其中第(①个图形中一共有3个△,第②个图形中一共有8个△,第③个图形中一共有14个△,…,按此规律排列下去,第⑨个图形中的△个数为( )
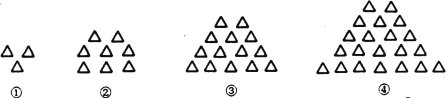
A. 54B. 61C. 71D. 77
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com