
科目: 来源: 题型:
【题目】如图一,点![]() 在线段
在线段![]() 上,图中有三条线段
上,图中有三条线段![]() 、
、![]() 和
和![]() ,若其中一条线段的长度是另外一条线段长度的
,若其中一条线段的长度是另外一条线段长度的![]() 倍,则称点
倍,则称点![]() 是线段
是线段![]() 的“巧点”.
的“巧点”.
(1)填空:线段的中点 这条线段的巧点(填“是”或“不是”或“不确定是”)
(问题解决)
(2)如图二,点![]() 和
和![]() 在数轴上表示的数分别是
在数轴上表示的数分别是![]() 和
和![]() ,点
,点![]() 是线段
是线段![]() 的巧点,求点
的巧点,求点![]() 在数轴上表示的数。
在数轴上表示的数。
(应用拓展)
(3)在(2)的条件下,动点![]() 从点
从点![]() 处,以每秒
处,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 向点
向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 向点
向点![]() 匀速运动,当其中一点到达中点时,两个点运动同时停止,当
匀速运动,当其中一点到达中点时,两个点运动同时停止,当![]()
![]() 、
、![]() 三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间
三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间![]() 的所有可能值.
的所有可能值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,ABCD的顶点的坐标分别为A(﹣6,9),B(0,9),C(3,0),D(﹣3,0),抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)过A、B两点,顶点为M.
(1)若抛物线过点C,求抛物线的解析式;
(2)若抛物线的顶点M落在△ACD的内部(包括边界),求a的取值范围;
(3)若a<0,连结CM交线段AB于点Q(Q不与点B重合),连接DM交线段AB于点P,设S1=S△ADP+S△CBQ , S2=S△MPQ , 试判断S1与S2的大小关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,等腰![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]()
(1)求证:![]() 是等边三角形
是等边三角形
(2)如图2,在![]() 内有一点
内有一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的度数
的度数
(3)如图3,在(2)的条件下,在![]() 外有一点
外有一点![]() ,连接
,连接![]() 、
、![]() 、若
、若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.



查看答案和解析>>
科目: 来源: 题型:
【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),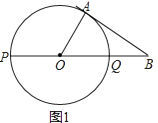
(1)当线段AB所在的直线与圆O相切时,求弧AQ的长(图1);
(2)若∠AOB=120°,求AB的长(图2);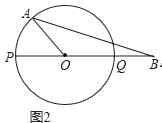
(3)如果线段AB与圆O有两个公共点A、M,当AO⊥PM于点N时,求tan∠MPQ的值(图3).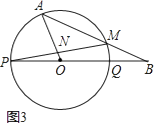
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:
单价(元/件) | 25 | 28 | 35 | 40 | 42 |
销量(件) | 50 | 44 | 30 | 20 | 16 |
(1)通过对上面表格中的数据进行分析,发现销量y(件)与单价x(元/件)之间存在一次函数关系,求y关于x的函数关系式(不需要写出函数自变量的取值范围);
(2)预计在今后的销售中,销量与单价仍然存在(1)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店销售![]() 两种商品,每件的售价分别为
两种商品,每件的售价分别为![]() 元、
元、![]() 元,五一期间,该商店决定对这两种商品进行促销活动,如图所示,若小红打算到该商店购买
元,五一期间,该商店决定对这两种商品进行促销活动,如图所示,若小红打算到该商店购买![]() 件
件![]() 商品和
商品和![]() 件
件![]() 商品,根据以上信息,请:
商品,根据以上信息,请:

(1)分别用含的代数式表示按照方案一和方案二所需的费用![]() 和
和![]() ;
;
(2)就![]() 的不同取值,请说明选择那种方案购买更实惠(两种优惠方案不能同时享受)
的不同取值,请说明选择那种方案购买更实惠(两种优惠方案不能同时享受)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC=6,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
(1)求BH的长;
(2)若AB=12,试判断∠CBD与∠A的数量关系,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com