
科目: 来源: 题型:
【题目】如图,抛物线y=a(x﹣1)(x﹣3)与x轴交于A,B两点,与y轴的正半轴交于点C,其顶点为D.
(1)写出C,D两点的坐标(用含a的式子表示);
(2)设S△BCD:S△ABD=k,求k的值;
(3)当△BCD是直角三角形时,求对应抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课![]() 分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为 理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数
分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为 理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数![]() 随时间
随时间![]() (分钟)的变化规律如图所示(其中
(分钟)的变化规律如图所示(其中![]() 都为线段)
都为线段)
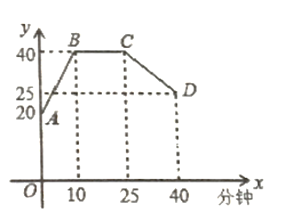
(1)分别求出线段![]() 和
和![]() 的函数解析式;
的函数解析式;
(2)开始上课后第![]() 分钟时与第
分钟时与第![]() 分钟时相比较,何时学生的注意力更集中?
分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲![]() 分钟,为了效果较好,要求学生的注意力指标数最低达到
分钟,为了效果较好,要求学生的注意力指标数最低达到![]() 那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(﹣2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.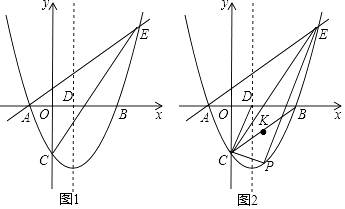
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某县为了了解2018年初中毕业生毕业后的去向,对部分九年级学生进行了抽样调查,就九年级学生的四种去向(A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他)进行数据统计,并绘制了两幅不完整的统计图(如图①②)请问:

(1)本次共调查了_ 名初中毕业生;
(2)请计算出本次抽样调查中,读职业高中的人数和所占百分比,并将两幅统计图中不完整的部分补充完整;
(3)若该县2018年九年级毕业生共有![]() 人,请估计该县今年九年级毕业生读职业高中的学生人数.
人,请估计该县今年九年级毕业生读职业高中的学生人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=![]() x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
(1)求m的值及抛物线的函数表达式;
(2)若P是抛物线对称轴上一动点,△ACP周长最小时,求出P的坐标;
(3)是否存在抛物在线一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若不存在,请说明理由;
(4)在(2)的条件下过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问![]() 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C ![]() 在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】解答题
(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M,求证:AE=BF; 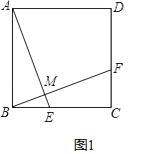
(2)如图2,将 (1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF于点M,探究AE与BF的数量关系,并证明你的结论. 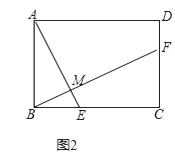
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE. 
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com