
科目: 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
查看答案和解析>>
科目: 来源: 题型:
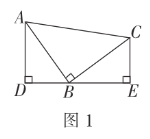
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).

查看答案和解析>>
科目: 来源: 题型:
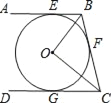
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】建华小区准备新建50个停车位,以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位需0.5万元;新建3个地上停车位和2个地下停车位需1.1万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)若该小区预计投资金额超过10万元而不超过11万元,则共有几种建造方案?
(3)已知每个地上停车位月租金100元,每个地下停车位月租金300元. 在(2)的条件下,新建停车位全部租出.若该小区将第一个月租金收入中的3600元用于旧车位的维修,其余收入继续兴建新车位,恰好用完,请直接写出该小区选择的是哪种建造方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E.F.G.H,顺次连接EF.FG.GH.HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH的形状是 ,证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)结合问题(2),请做出图形并且证明
查看答案和解析>>
科目: 来源: 题型:
【题目】一个装有进水管和出水管的容器,根据实际需要,从某时刻开始的2分钟内只进水不出水,在随后的4分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图所示.
(1)当2≤x≤6时,求y与x的表达式;
(2)请将图象补充完整;
(3)从进水管开始进水起,求该容器内的水量不少于7.5升所持续时间.

查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证:![]() .
.
(2)如图2,已知点![]() ,点
,点![]() ,
,![]() ,
,![]() ,且点
,且点![]() 在第一象限,求
在第一象限,求![]() 所在直线的表达式.
所在直线的表达式.
(3)如图3,在长方形![]() 中,
中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 分别在坐标轴上,点
分别在坐标轴上,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在
上的动点且在![]() 轴的右侧.若
轴的右侧.若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,请求出点
为直角顶点的等腰直角三角形,请求出点![]() 的坐标.
的坐标.


查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产![]() 两种设备,已知每台
两种设备,已知每台![]() 种设备的成本是
种设备的成本是![]() 种设备的1.5倍,公司若投入6万元生产
种设备的1.5倍,公司若投入6万元生产![]() 种设备,投人15万元生产
种设备,投人15万元生产![]() 种设备,则可生产两种设备共40台.请解答下列问题:
种设备,则可生产两种设备共40台.请解答下列问题:
(1)![]() 两种设备每台的成本分别是多少万元?
两种设备每台的成本分别是多少万元?
(2)若![]() 两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中
两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中![]() 种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润.
种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com