
科目: 来源: 题型:
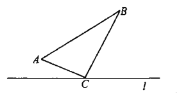
【题目】如图,![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发沿
出发沿![]() 路径向终点
路径向终点![]() 运动;点
运动;点![]() 从
从![]() 点出发沿
点出发沿![]() 路径向终点
路径向终点![]() 运动.点
运动.点![]() 和
和![]() 分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过
分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过![]() 和
和![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .则点
.则点![]() 运动时间等于____________时,
运动时间等于____________时,![]() 与
与![]() 全等。
全等。
查看答案和解析>>
科目: 来源: 题型:
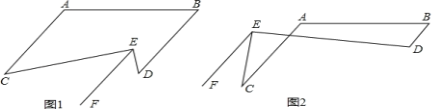
【题目】已知:∠A=(90+x)°,∠B=(90﹣x)°,∠CED=90°,射线EF∥AC,2∠C﹣∠D=m.(1)判断AC与BD的位置关系,并说明理由.
(2)如图1,当m=30°时,求∠C、∠D的度数.
(3)如图2,求∠C、∠D的度数(用含m的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】填空并完成以下证明:
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥ .( )
∴∠BAP= .( )
又∵∠1=∠2,(已知)
∠3= ﹣∠1,
∠4= ﹣∠2,
∴∠3= (等式的性质)
∴AE∥PF.( )
∴∠E=∠F.( )

查看答案和解析>>
科目: 来源: 题型:
【题目】为了参加“醴陵市中小学生首届诗词大会”,某中学八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77 ,92, 85;八(2)班79 ,85 ,92,85 ,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | d |
八(2) | a | 85 | 85 | e |
(1)直接写出表中a,b,c的值:a= ,b= ,c= .
(2)求d,e的值,并根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
(3)若“醴陵市中小学生首届诗词大会”中,各中学代表队成绩计分分两部分:现场评委记分和网络评委投票记分。且现场评委记分权数为80%,网络评委投票记分权数为20%,请计算A,B,C三所中学代表队的最终得分为多少?
中学A | 中学B | 中学C | |
评委记分 | 90 | 80 | 85 |
网络投票记分 | 85 | 92 | 88 |
查看答案和解析>>
科目: 来源: 题型:
【题目】“![]() 年冬季越野赛”在滨河学校操场举行,某运动员从起点学校东门出发,途径湿地公园,沿比赛路线跑回终点学校东门.沿该运动员离开起点的路程
年冬季越野赛”在滨河学校操场举行,某运动员从起点学校东门出发,途径湿地公园,沿比赛路线跑回终点学校东门.沿该运动员离开起点的路程![]() (千米)与跑步时间
(千米)与跑步时间![]() (时间)之间的函数关系如图所示,其中从起点到湿地公园的平均速度是
(时间)之间的函数关系如图所示,其中从起点到湿地公园的平均速度是![]() 千米/分钟,用时
千米/分钟,用时![]() 分钟,根据图像提供的信息,解答下列问题:
分钟,根据图像提供的信息,解答下列问题:
(![]() )求图中
)求图中![]() 的值;
的值;
(![]() )组委会在距离起点
)组委会在距离起点![]() 千米处设立一个拍摄点
千米处设立一个拍摄点![]() ,该运动员从第一次过点
,该运动员从第一次过点![]() 到第二次过点
到第二次过点![]() 所用的时间为
所用的时间为![]() 分钟.
分钟.
①求![]() 所在直线的函数解析式;
所在直线的函数解析式;
②该运动员跑完全程用时多少分钟?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将长方形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
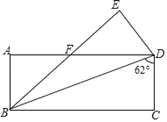
A. 62°B. 56°C. 31°D. 28°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com