
科目: 来源: 题型:
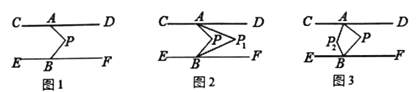
【题目】如图1,已知直线CD//EF ,点A、B分别在直线CD与EF上。P为两平行线间一点
(1)若∠DAP= 40° , ∠FBP=70°,求∠APB的度数是多少?
(2)直接写出∠DAP, ∠FBP, ∠APB之间有什么关系?
(3)利用(2)的结论解答:
①如图2, AP1、BP1,分别平分∠DAP,∠FBP,请你写出∠P与∠P1,的数量关系,并说明理由;
②如图3, AP2、 BP2分别平分∠CAP,∠EBP,若∠APB=β,求∠AP2B (用含β的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
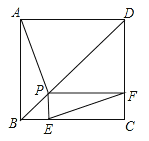
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
A. ①②③④ B. ①②④⑤ C. ②③④⑤ D. ①③④⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.

(1)根据题意,将下面的表格补充完整.

(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=OB=OC=6,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的![]() .
.
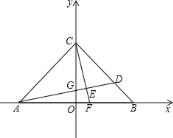
(1)求点D的坐标;
(2)过点C作CE⊥AD,交AB交于F,垂足为E.
①求证:OF=OG;
②求点F的坐标。
(3)在(2)的条件下,在第一象限内是否存在点P,使△CFP为等腰直角三角形?若存在,直接写出点P坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】【题目】某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.图示是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是反比例函数y=一的图象上一部分,请根据图中信息解答下列问题
(1)恒温系统在这天保持大棚内温度20℃的时间有多少小时?
(2)求k的值;

(3)当x=20时,大棚内的温度约为多少度?
查看答案和解析>>
科目: 来源: 题型:
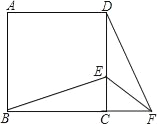
【题目】如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠BEC=60°,求∠EFD的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得的利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四边形ABCD中,∠ABC+∠ADC=180,连接AC,BD.
(1)如图1,当∠ACD=∠CAD=45时,求∠CBD的度数;
(2)如图2,当∠ACD=∠CAD=60时,求证:AB+BC=BD;
(3)如图3,在(2)的条件下,过点C作CK⊥BD于点K,在AB的延长线上取点F,使∠FCG=60,过点F作FH⊥BD于点H,BD=8,AB=5,GK=![]() ,求BH的长。
,求BH的长。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com