
科目: 来源: 题型:
【题目】已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-![]() x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
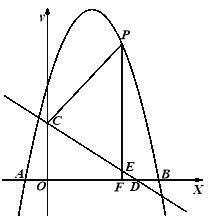
(1)求抛物线的解析式;(2)若PE=5EF,求m的值;(3)若点E′是点E关于直线PC的对称点、是否存在点P,使点E/落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
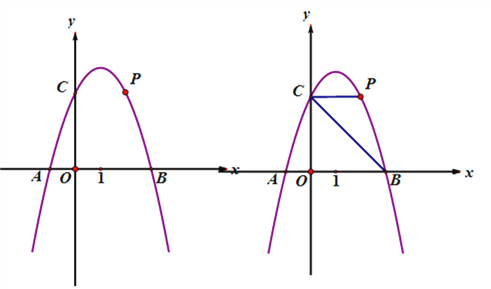
【题目】如图,抛物线![]() 交X轴于点A、B(A左B右),交Y轴于点C,
交X轴于点A、B(A左B右),交Y轴于点C, ![]()
=6,点P为第一象限内抛物线上的一点.
(1)求抛物线的解析式;
(2)若∠PCB=45°,求点P的坐标;
(3)点Q为第四象限内抛物线上一点,点Q的横坐标比点P的横坐标大1,连接PC、
AQ,当PC=![]() AQ时,求点P的坐标以及ΔPCQ的面积.
AQ时,求点P的坐标以及ΔPCQ的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)同题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.
小明想到一种方法,但是没有解答完:
如图2,过P作PE∥AB,∴∠APE+∠PAB=180°.
∴∠APE=180°-∠PAB=180°-130°=50°.
∵AB∥CD.∴PE∥CD.
…………
请你帮助小明完成剩余的解答.
(2)问题迁移:请你依据小明的思路,解答下面的问题:
如图3,AD∥BC,点P在射线OM上运动,∠MDP=∠α,∠BCP=∠β.
①当点P在A、B两点之间时,∠CPD,∠α,∠β之间有何数量关系?请说明理由.
②当点P在A、B两点外侧时(点P与点O不重合),请直接写出∠CPD,∠α,∠β之间的数量关系.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.

(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】庆元大道两侧需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
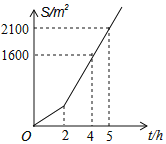
A. 200B. 300C. 400D. 500
查看答案和解析>>
科目: 来源: 题型:
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.连接DG,BE,易得DG=BE且DG⊥BE(不需要说明理由)
的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.连接DG,BE,易得DG=BE且DG⊥BE(不需要说明理由)
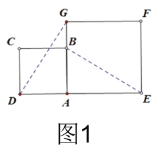
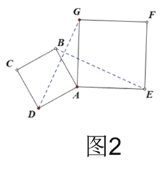
(1)如图2,小明将正方形ABCD绕点A逆时针旋转,旋转角为![]() (30﹤
(30﹤![]() ﹤180)
﹤180)
①连接DG,BE,求证:DG=BE且DG⊥BE;
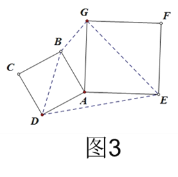
②在旋转过程中,如图3,连接BG,GE,ED,DB,求出四边形BGED面积的最大值.
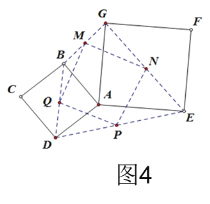
(2)如图4,分别取BG,GE,ED,DB的中点M,N,P,Q,连接MN,NP,PQ,QM,则四边形MNPQ的形状为 ,四边形MNPQ面积的最大值是 ,
查看答案和解析>>
科目: 来源: 题型:
【题目】某商厦进货员预测一种应季衬衫能畅销市场,就用0.8万元购进这种衬衫,面市后果然供不应求.于是,商厦又用1.76万元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了4元,商厦销售这种衬衫时每件预定售价都是58元.
(1)求这种衬衫原进价为每件多少元?
(2)经过一段时间销售,根据市场饱和情况,商厦经理决定对剩余的100件衬衫进行打折销售,以提高回款速度,要使这两批衬衫的总利润不少于6300元,最多可以打几折?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com