
科目: 来源: 题型:
【题目】《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著 .是《算经十书》中最重要的一部,成于公元一世纪左右 .全书总结了战国、秦、汉时期的数学成就 .同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首先记录了盈不足等问题,其中有一个数学问题“今有垣厚一丈,两鼠对穿 .大鼠日一尺,小鼠亦一尺 .大鼠日自倍,小鼠日自半 .问:何日相逢?”.译文:“有一堵一丈(旧制长度单位,1丈=10尺=100寸)厚的墙,两只老鼠从两边向中间打洞 .大老鼠第一天打一尺,小老鼠也是一尺 .大老鼠每天的打洞进度是前一天的一倍,小老鼠每天的进度是前一天的一半 .问它们几天可以相逢?”请你用所学数学知识方法给出答案:______________ .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

查看答案和解析>>
科目: 来源: 题型:
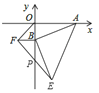
【题目】如图,点A的坐标为(8,0),点B为y轴负半轴上的一动点,分别以OB,AB为直角边在第三、第四象限作等腰直角三角形OBF,等腰直角三角形ABE,连接EF交y轴与P点,当点B在y轴上移动时,则PB的长度是( )
A.2B.4C.不是已知数的定值D.PB的长度随点B的运动而变化
查看答案和解析>>
科目: 来源: 题型:
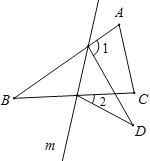
【题目】如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是( )
A. 32° B. 64° C. 65° D. 70°
查看答案和解析>>
科目: 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).
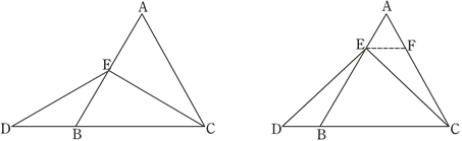
图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目: 来源: 题型:
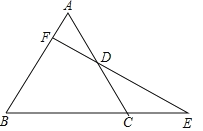
【题目】如图,△ABC是等边三角形,延长BC到E,使CE=![]() BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
BC.点D是边AC的中点,连接ED并延长ED交AB于F,求证:
(1)EF⊥AB;(2)DE=2DF.
查看答案和解析>>
科目: 来源: 题型:
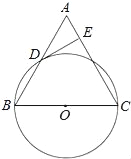
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场销售的篮球和足球的进货价格分别是每个30元,40元.商场销售5个篮球和1个足球,可获利76元;销售6个篮球和3个足球,可获利120元.
(1)求该商场篮球和足球的销售价格分别是多少?
(2)商场准备用不多于2500元的资金购进篮球和足球共70个,问最少需要购进篮球多少个?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() 与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).
(1)求a,m的值;
(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,CD⊥DA,DA⊥AB,∠1=∠2.试确定射线DF与AE的位置关系,并说明你的理由.

(1)问题的结论:DF______AE.
(2)证明思路欲证DF______AE,只要证∠3=______.
(3)证明过程:
证明:∵CD⊥DA,DA⊥AB,( )
∴∠CDA=∠DAB=______°(垂直定义)
∵∠1=∠2,( )
∴∠CDA-∠1=______-______,(等式的性质)
即∠3=______
∴DF______AE( , )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com