
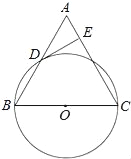
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=![]() ,求DE的长.
,求DE的长.
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 边的垂直平分线
边的垂直平分线![]() 交
交![]() 于点
于点![]() ,
,![]() 边的垂直平分线
边的垂直平分线![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,联结
,联结![]() 、
、![]() ,若
,若![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() .
.

(1)求线段![]() 的长;
的长;
(2)联结![]() ,求线段
,求线段![]() 的长;
的长;
(3)若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了统计表如下:

零花钱数额(元) | 5 | 10 | 15 | 20 |
学生个数(个) | a | 15 | 20 | 5 |
请根据表中的信息,回答以下问题.
(1)求a的值;
(2)求这50名学生每人一周内的零花钱额的众数、中位数和平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题成立的是( ).
A.全等三角形的对应角相等
B.若三角形的三边满足![]() ,则该三角形是直角三角形
,则该三角形是直角三角形
C.对顶角相等
D.同位角互补,两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.
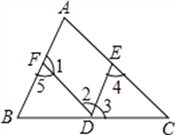
(1)∵DE∥AB,( 已知 )
∴∠2= . ( , )
(2)∵DE∥AB,(已知 )
∴∠3= .( , )
(3)∵DE∥AB(已知 ),
∴∠1+ =180°.( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张明和李强两名运动爱好者周末相约到东湖绿道进行跑步锻炼.(1)周日早上6点,张明和李强同时从家出发,分别骑自行车和步行到离家距离分别为4.5千米和1.2千米的绿道落雁岛入口汇合,结果同时到达,且张明每分钟比李强每分钟多行220米,求张明和李强的速度分别是多少米/分?
(1)两人到达绿道后约定先跑 6 千米再休息,李强的跑步速度是张明跑步速度的m倍,两人在同起点,同时出发,结果李强先到目的地n分钟.
①当m=12,n=5时,求李强跑了多少分钟?
②张明的跑步速度为 米/分(直接用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com