
科目: 来源: 题型:
【题目】如图,已知点![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 在线段
在线段![]() 上,
上,![]() 与
与![]() 交于点
交于点![]() ,
,![]() .求证:
.求证:![]() .(完成以下填空)
.(完成以下填空)
证明:∵![]() (已知),
(已知),
且![]() ( )
( )
∴![]() (等量代换)
(等量代换)
∴ ![]() ( )
( )
∴![]() ( )
( )
又∵![]() (已知)
(已知)
∴![]() (等量代换)
(等量代换)
∴![]() ( )
( )

查看答案和解析>>
科目: 来源: 题型:
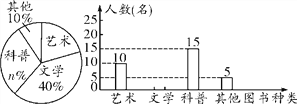
【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他.随机调查了该校m名学生(每名学生必选且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:

根据统计图提供的信息,解答下列问题:
(1)m= ,n= ;
(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度;
(3)请根据以上信息补全条形统计图;
(4)根据抽样调查的结果,请你估计该校1000名学生中有多少学生最喜欢科普类图书.
【答案】 (1)m=50, n=30;(2)72度 (3)补图见解析(4)300
【解析】试题分析:(1)根据其他的人数和所占的百分比即可求得m的值,从而可以求得n的值;
(2)根据扇形统计图中的数据可以求得“艺术”所对应的扇形的圆心角度数;
(3)根据题意可以求得喜爱文学的人数,从而可以将条形统计图补充完整;
(4)根据统计图中的数据可以估计该校600名学生中有多少学生最喜欢科普类图书.
试题解析:
解:(1)m=5÷10%=50,n%=15÷50=30%,
故答案为:50,30;
(2)由题意可得,
“艺术”所对应的扇形的圆心角度数是:360°×![]() =72°,
=72°,
故答案为:72;
(3)文学有:50-10-15-5=20,
补全的条形统计图如图所示;

(4)由题意可得,
600×![]() =180,
=180,
即该校600名学生中有180名学生最喜欢科普类图书.
点睛:本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
【题型】解答题
【结束】
23
【题目】端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.5元,花35元购买粽子的个数与花20元购买咸鸭蛋的个数相同.粽子与咸鸭蛋的价格各是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.
方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题:
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当20<y<30时,求t的取值范围;
(3)分别求出甲,乙行驶的路程S甲,S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;
(4)丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过![]() h与乙相遇,问丙出发后多少时间与甲相遇?
h与乙相遇,问丙出发后多少时间与甲相遇?

查看答案和解析>>
科目: 来源: 题型:
【题目】某商店销售一种旅游纪念品,第一周的营业额为200元,第二周该商店对纪念品打8折销售,结果销售量增加3件,营业额增加了40%.
(1)求该商店第二周的营业额;
(2)求第一周该种纪念品每件的销售价格.
查看答案和解析>>
科目: 来源: 题型:
【题目】先化简,再求值![]() ,其中
,其中![]() 的值从不等式组
的值从不等式组![]() 的整数解中选取.
的整数解中选取.
【答案】(a-2)2.
【解析】试题分析:根据分式的减法和除法可以化简题目中的式子,然后在不等式组![]() 的解集中选取一个使得原分式有意义的整数值代入化简后的式子即可解答本题.
的解集中选取一个使得原分式有意义的整数值代入化简后的式子即可解答本题.
试题解析:
解:原式=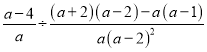
=![]()
=![]()
=(a-2)2,
由不等式组![]() 得,0≤a<5.5,
得,0≤a<5.5,
∴当a=1时,原式=(1-2)2=1.
点睛:本题考查分式的化简求值、一元一次不等式组的整数解,解答本题的关键是明确分式化简求值的方法,会求一元一次不等式组的解集.
【题型】解答题
【结束】
22
【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他.随机调查了该校m名学生(每名学生必选且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(1)m= ,n= ;
(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度;
(3)请根据以上信息补全条形统计图;
(4)根据抽样调查的结果,请你估计该校1000名学生中有多少学生最喜欢科普类图书.
查看答案和解析>>
科目: 来源: 题型:
【题目】解分式方程:
(1) ![]() (2)
(2) ![]()
【答案】(1) ![]() ;(2)x=
;(2)x=![]()
【解析】试题分析:(1)两边乘以(x-1)(2x+1)去分母,转化为整式方程,然后解整式方程,检验后写出分式方程的解即可;
(2)两边乘以(x+2)(x-2)去分母,转化为整式方程,然后解整式方程,检验后写出分式方程的解即可.
试题解析:
解:(1)两边乘以(x-1)(2x+1)去分母得:2x+1=5(x-1),
解得:x=2,
当x=2时,(x-1)(2x+1)≠0,
∴原分式方程的解为x=2;
(2)两边乘以(x+2)(x-2)去分母得:(x-2)2-3=(x+2)(x-2),
解得:x=![]() ,
,
当x=![]() 时,(x+2)(x-2)≠0,
时,(x+2)(x-2)≠0,
所以原分式方程的解为x=![]() .
.
【题型】解答题
【结束】
21
【题目】先化简,再求值![]() ,其中
,其中![]() 的值从不等式组
的值从不等式组![]() 的整数解中选取.
的整数解中选取.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)求证:AC2=COCP;
(3)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.

查看答案和解析>>
科目: 来源: 题型:
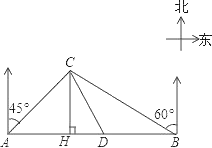
【题目】某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
(1)求牧民区C到B地的距离(结果用根式表示);
(2)一天,乙医疗队的医生要到牧民区C出诊,她先由B地搭车沿公路AB到D处(BD<AB)转车,再由D地沿DC方向到牧民区C.若C、D两地距离是B、C两地距离的![]() 倍,求B、D两地的距离.(结果精确到0.1千米 参考数据:
倍,求B、D两地的距离.(结果精确到0.1千米 参考数据: ![]() ≈2.449,
≈2.449, ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目: 来源: 题型:
【题目】计算:
(1)![]() (2)
(2) ![]()
(3) ![]() (4)
(4) 
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ; (4)
; (4) ![]()
【解析】试题分析:(1)分子、分母分解因式后约分即可;
(2)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可;
(3)第二个分式分子、分母分解因式后约分,然后通分转化为同分母分式,最后依照同分母分式的加减法则计算即可;
(4)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可.
试题解析:
解:(1)原式=
=![]() ;
;
(2)原式=![]()
=![]()
=![]() ;
;
(3)原式=![]()
=![]()
=![]()
=![]()
=![]() ;
;
(4)原式=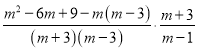
=![]()
=![]() .
.
点睛:此题考查了分式的混合运算,熟练掌握运算法则和运算顺序是解本题的关键.
【题型】解答题
【结束】
20
【题目】解分式方程:
(1) ![]() (2)
(2) ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com