【题目】已知二次函数的图像，有下列4个结论：①＞0；②；③； ④其中正确的结论有_______．(填序号）

【题目】如图，在等边三角形ABC中，BC=6,射线AG∥BC，点E从点A出发沿射线AG以的速度运动，同时点F从点B出发沿射线BC以的速度运动，设运动时间为

（1）连接EF，当EF经过AC边的中点D时，求证：△ADE≌△CDF

（2）填空：

①当为 s时，四边形ACFE是菱形；

②当为 s时，以A，F，C，E为顶点的四边形是直角梯形．

（1）若MN与坐标轴平行，则MN＝　 　；

（2）若m、n、t满足，MA⊥x轴，垂足为A，NB⊥x轴，垂足为B．

①求四边形MABN的面积；

②连接MN、OM、ON，若△MON的面积大于26而小于30，求m的取值范围．

（1）四边形EFGH的形状是_______，证明你的结论．

（2）连接四边形ABCD的对角线AC与BD，当AC与BD满足____条件时，四边形EFGH是矩形；（只需要写结论，不需证明）

（3）连接四边形ABCD的对角线AC与BD，当AC与BD满足______条件时，四边形EFGH是菱形．（只需要写结论，不需证明）

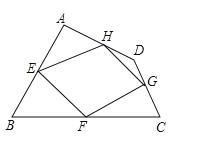
（1）四边形EFGH的形状是什么，并证明你的结论．

（2）当四边形ABCD的对角线满足什么条件时，四边形EFGH是矩形；并利用你给的条件加以证明．

【题目】已知反比例函数y＝ (m为常数，且m≠5)．

(1)若在其图象的每个分支上，y随x的增大而增大，求m的取值范围；

(2)若其图象与一次函数y＝－x＋1的图象的一个交点的纵坐标是3，求m的值．

（1）请求出小欣在这次采购中，“雀巢巧克力”和“趣多多小饼干”各买了多少包？

（2）“五一”期间，小欣发现，A、B两超市以同样的价格出售同样的商品，并且又各自推出不同的优惠方案：在A超市累计购物超过50元后，超过50元的部分打九折；在B超市累计购物超过100元后，超过100元的部分打八折．

①请问“五一”期间，若小欣购物金额超过100元，去哪家超市购物更划算？

②“五一”期间，小欣又到“B超市”购买了一些“雀巢巧克力”，请问她至少购买多少包时，平均每包价格不超过20元？

（1）画出△ABC；

（2）△A′B′C′是△ABC经过平移得到的，△ABC中任意一点P（x1，y1）平移后的对应点为P′（x1+5，y1+3）．画出平移后的△A′B′C′，并求△A′B′C′的面积；

（3）设直线A′C′与x轴交于点Q，求交点Q坐标．

【题目】能判定四边形是平行四边形的是（ ）

A.AB∥CD，B. AB∥CD，

C.，D.，