
科目: 来源: 题型:
【题目】如图,三个边长均为4的正方形重叠在一起,O1,O2是其中左侧两个正方形的对角线交点,同时O1,O2也是右侧两个正方形的顶点,根据教材第63页《实践与探究》活动中有关内容,可知阴影部分面积是( )

A.2B.4C.6D.8
查看答案和解析>>
科目: 来源: 题型:
【题目】计算
(1)12-(-18)+(-7)-15
(2)(-2.7)+(+1![]() )-(-6.7)+(-1.6)
)-(-6.7)+(-1.6)
(3)20+(-14)-(-18)-13
(4)81÷|-2![]() |×
|×![]()
(5)![]()
(6)-14-(1-0.5×![]() )×(2-23)
)×(2-23)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.


(1)当![]() 时,
时,![]() = ,
= ,![]() = ;点
= ;点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐 (填“增大”或“减小”);
逐渐 (填“增大”或“减小”);
(2)当![]() 等于多少时,
等于多少时,![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出![]() 的度数.若不可以,请说明理由.
的度数.若不可以,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:① DC = BC; ②AD+AB=AC.请你证明结论②;
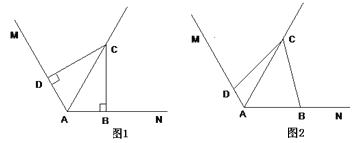
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表是中国电信两种“![]() 套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)
套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)
月基本费/元 | 主叫通话/分钟 | 上网流量/MB | 接听 | 主叫超时(元/分钟) | 超出流量(元/MB) | |
套餐1 | 49 | 200 | 500 | 免费 | 0.20 | 0.3 |
套餐2 | 69 | 250 | 600 | 免费 | 0.15 | 0.2 |
(1)6月小王主叫通话时间220分钟,上网流量800MB.按套餐1计费需 元,按套餐2计费需 元;
若他按套餐2计费需129元,主叫通话时间为240分钟,则他上网使用了 MB流量;
(2)若上网流量为540MB,是否存在某主叫通话时间![]() (分钟),按套餐1和套餐2的计费相等?若存在,请求出
(分钟),按套餐1和套餐2的计费相等?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,△ABC为等边三角形,点E、F分别在BC和AB上,且CE=BF,AE与CF相交于点H.
(1)求证:△ACE≌△CBF;
(2)求∠CHE的度数;
(3)如图2,在图1上以AC为边长再作等边△ACD,将HE延长至G使得HG=CH,连接HD与CG,求证:HD=AH+CH

查看答案和解析>>
科目: 来源: 题型:
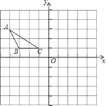
【题目】已知:如图,在△ABC中,点A的坐标为(﹣4,3),点B的坐标为(﹣3,1),BC=2,BC∥x轴.
(1)画出△ABC关于y轴对称的图形△A1B1C1;并写出A1,B1,C1的坐标;
(2)求以点A、B、B1、A1为顶点的四边形的面积.
查看答案和解析>>
科目: 来源: 题型:
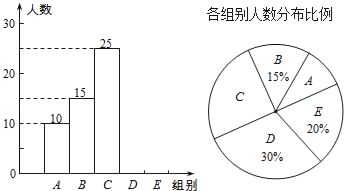
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com