（每组可含最低值，不含最高值）

请根据上述信息，回答下列问题：

（1）你认为哪位学生抽取的样本具有代表性？_____．

估计该校全体八年级学生平均每周上网时间为_____h；

（2）在具有代表性的样本中，中位数所在的时间段是_____h/周；

（3）专家建议每周上网2h以上（含2h）的同学应适当减少上网的时间，根据具有代表性的样本估计，该校全体八年级学生中有多少名学生应适当减少上网的时间？

A.2+B.C.D.3

【题目】如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点C.抛物线经过A，C两点，且与x轴交于另一点B（点B在点A右侧）．

（1）求抛物线的解析式及点B坐标；

（2）若点M是线段BC上的一动点，过点M的直线EF平行y轴交x轴于点F，交抛物线于点E.求ME长的最大值；

（3）试探究当ME取最大值时，在抛物线上、x轴下方是否存在点P，使以M，F，B，P为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，试说明理由．

根据上表回答问题：

（1）星期二收盘时，该股票每股______元.

（2）本周内股票收盘时的最高价______元.

（3）已知买入股票与卖出股票均需支付成交金额的千分之五的交易费，若小王在本周五以收盘价将全部股票卖出，他的收益情况如何？

（1）求证：①△ABG≌△AFG； ②求GC的长；

（2）求△FGC的面积．

（1）每件甲商品与每件乙商品的售价分别是多少元？

（2）若甲、乙两种商品的进货总投入不超过4200元，则至多进货甲商品多少件？

（3）若这批商品全部售完，该商店至少盈利多少元？

【题目】如图，已知△ABC中，∠C=90°，AC=BC=，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B，求C′B的长度.

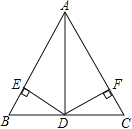
（1）请写出与A点有关的三个正确结论；

（2）DE与DF在数量上有何关系？并给出证明．

【题目】如图，在Rt△ABC 中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ABE绕点顺时针旋转90后，得到△ACF，连接DF．下列结论中：①∠DAF=45° ②△≌△ ③AD平分∠EDF ④；正确的有______________（填序号）

（1）当点B在x轴正半轴上运动时，求点C点的坐标．（用m表示）

（2）当m=0时，如图2，P为OA上一点，过点P作PM⊥PC，PM=PC，连MC交OD于点N，求AM+2DN的值；

（3）如图3，在第（2）问的条件下，E、F分别为CD、CO上的点，作EG∥x轴交AO于G，作FH∥y轴交AD于H，K是EG与FH的交点．若S四边形KFCE=2S四边形AGKH，试确定∠EAF的大小，并证明你的结论．