
科目: 来源: 题型:
【题目】如图,点P是边长为![]() 的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是
的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是![]() .其中正确结论是( )
.其中正确结论是( )

A. ①③ B. ②③ C. ②③④ D. ②④
查看答案和解析>>
科目: 来源: 题型:
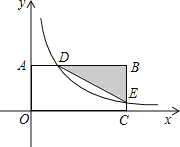
【题目】如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数![]() 的图象分别交BA,BC于点D,E当AD:BD=1:3且
的图象分别交BA,BC于点D,E当AD:BD=1:3且![]() 的面积为18时,则k的值是__________________
的面积为18时,则k的值是__________________
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是一套房子的平面图,尺寸如图.
![]() 这套房子的总面积是多少?
这套房子的总面积是多少? ![]() 用含有x、y的代数式表示
用含有x、y的代数式表示![]() .
.
![]() 如果
如果![]() 米,
米, ![]() 米,那么房子的面积是多少平方米?如果每平方米房价为
米,那么房子的面积是多少平方米?如果每平方米房价为![]() 万元,那么房屋总价多少万元?
万元,那么房屋总价多少万元?

查看答案和解析>>
科目: 来源: 题型:
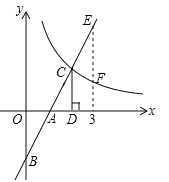
【题目】(3分)如图,在直角坐标系中,直线![]() 与坐标轴交于A、B两点,与双曲线
与坐标轴交于A、B两点,与双曲线![]() (
(![]() )交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
①![]() ;
;
②当0<x<3时,![]() ;
;
③如图,当x=3时,EF=![]() ;
;
④当x>0时,![]() 随x的增大而增大,
随x的增大而增大,![]() 随x的增大而减小.
随x的增大而减小.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:
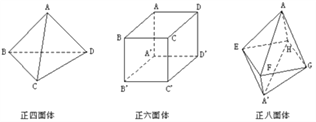
⑴填空:
①正四面体的顶点数V= ,面数F= ,棱数E= .
②正六面体的顶点数V= ,面数F= ,棱数E= .
③正八面体的顶点数V= ,面数F= ,棱数E= .
⑵若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用一个公式来表示,这就是著名的欧拉公式,请写出欧拉公式:
⑶如果一个多面体的棱数为30,顶点数为20,那么它有多少个面?
查看答案和解析>>
科目: 来源: 题型:
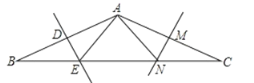
【题目】如图,在ΔABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N.
(1)求△AEN的周长;
(2)判断ΔAEN的形状并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目: 来源: 题型:
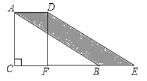
【题目】如图,在RtΔABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB方向向右平移得到△DEF.若四边形ABED的面积为8,则平移距离为__.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com