
科目: 来源: 题型:
【题目】把下列各数填在相应的大括号内:
﹣5,|-![]() |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),![]()
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
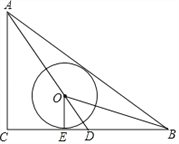
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
查看答案和解析>>
科目: 来源: 题型:
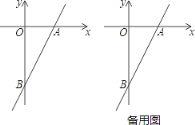
【题目】如图,平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图线与坐标轴分别交于点A、B、C,其中点A(0,8),OB=
x2+bx+c的图线与坐标轴分别交于点A、B、C,其中点A(0,8),OB=![]() OA.
OA.
(1)求二次函数的表达式;
(2)若OD=OB,点F为该二次函数在第二象限内图象上的动点,E为DF的中点,当△CEF的面积最大时,求出点E的坐标;
(3)将三角形CEF绕E旋转180°,C点落在M处,若M恰好在该抛物线上,求出此时△CEF的面积.


查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数y=2x-4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1,d2。
(1)求点A,B的坐标;
(2)当P为线段AB的中点时,求d1+d2的值;
(3)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;
(4)若在线段AB上存在无数个点P,使d1+ad2=4(a为常数),求a的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】提出问题:
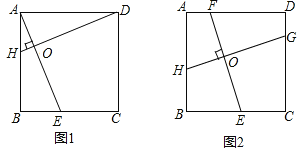
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在数轴上A点表示数﹣2,B点表示数6,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过 秒,甲、乙两小球到原点的距离相等.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)|﹣2![]() |+|﹣3
|+|﹣3![]() |
|
(2)8.63﹣(﹣1.37)
(3)(﹣25)+34+156+(﹣65)
(4)(﹣0.5)﹣2![]() ﹣(+2
﹣(+2![]() )
)
(5)(﹣52)+24﹣(+74)+12.
(6)﹣![]() ﹣(﹣
﹣(﹣![]() )+(﹣
)+(﹣![]() )﹣(+
)﹣(+![]() )
)
(7)(+![]() )+(﹣
)+(﹣![]() )﹣(+
)﹣(+![]() )﹣(﹣
)﹣(﹣![]() )
)
查看答案和解析>>
科目: 来源: 题型:
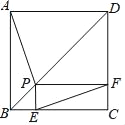
【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为![]() ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
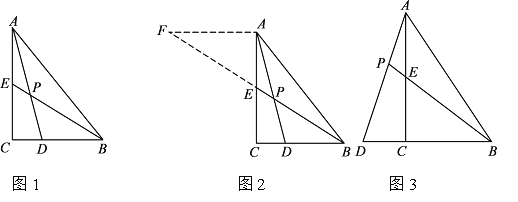
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com