【题目】已知抛物线y=a（x+3）（x﹣1）（a≠0），与x轴从左至右依次相交于A、B两点，与y轴相交于点C，经过点A的直线y=﹣x+b与抛物线的另一个交点为D．

（1）若点D的横坐标为2，求抛物线的函数解析式；

（2）若在第三象限内的抛物线上有点P，使得以A、B、P为顶点的三角形与△ABC相似，求点P的坐标；

（3）在（1）的条件下，设点E是线段AD上的一点（不含端点），连接BE．一动点Q从点B出发，沿线段BE以每秒1个单位的速度运动到点E，再沿线段ED以每秒个单位的速度运动到点D后停止，问当点E的坐标是多少时，点Q在整个运动过程中所用时间最少？

（1）集合{﹣4，12}是否是条件集合？

（2）集合{，﹣，}是否是条件集合？

（3）若集合{8，n}和{m}都是条件集合．求m、n的值．

（1）求该学校为新增电脑投资的年平均增长率；

（2）从2016年到2018年，该中学三年为新增电脑共投资多少万元？

(1)这次被调查的市民共有多少人？

(2)请你将统计图1补充完整；

(3)求图2中D项目对应的扇形的圆心角的度数．

【题目】已知：如图，四边形ABCD为矩形，，，点E是CD的中点，点P在AB上以每秒2个单位的速度由A向B运动，设运动时间为t秒．

（1）当点P在线段AB上运动了t秒时，__________________（用代数式表示）;

（2）t为何值时，四边形PDEB是平行四边形：

（3）在直线AB上是否存在点Q，使以D、E、Q、P四点为顶点的四边形是菱形？若存在，求出t的值：若不存在，说明理由．

（1）第一个框框住的三个数中最小的数为a,三个数的和是: ；第二个框框住的三个数中最小的数为b,三个数的和是: ；第三个框框住的三个数中最小的数为c,三个数的和是: ；

（2）这三个框框住的数的和能是48吗？，能，求出最小的数a、b、c的值.

【题目】如图，在矩形ABCD中， ，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：① ∠AED=∠CED；② OE=OD；③ BH=HF；④ BC-CF=2HE；⑤ AB=HF，其中正确的有（　　）

A. 2个 B. 3个 C. 4个 D. 5个

（1）某品牌太阳镜由一个镜架和两个镜片配套构成，每个工人每天可以加工个镜架或者加工个镜片，现有名工人，应怎么安排人力，才能使每天生产的镜架和镜片配套？能做成多少副太阳镜？

（2）去年春季，蔬菜种植场在公顷的大棚地里分别种植了茄子和西红柿，总费用是万元.其中，种植茄子和西红柿每公顷的费用和每公顷获利情况如表：

请解答下列问题：

①求出茄子和西红柿的种植面积各为多少公顷？

②种植场在这一季共获利多少万元？

【题目】如图，正方形，点是线段延长线一点，连结，，

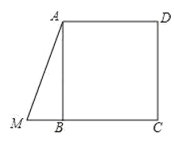
（1）将线段沿着射线运动，使得点与点重合，用代数式表示线段扫过的平面部分的面积.

（2）将三角形绕着点旋转，使得与重合，点落在点，用代数式表示线段扫过的平面部分的面积.

（3）将三角形顺时针旋转，使旋转后的三角形有一边与正方形的一边完全重合（第（2）小题的情况除外），请在如图中画出符合条件的3种情况，并写出相应的旋转中心和旋转角