（1）a的值________，b的值________，c的值________．

（2）已知蚂蚁从A点出发，途径B，C两点，以每秒3cm的速度爬行，需要多长时间到达终点C？

（3）求值：a2b﹣bc．

（1）求上表中的的值；

（2）若该市居民乙某月交电费220元，居民乙当月的生活用电量为多少千瓦时？

（3）实行“阶梯电价”收费后，该市居民丙月用电量为多少千瓦时，其当月的平均电价为0.55元/千瓦时？

【题目】观察下列单项式：，，，，…，，…写出第个单项式，为了解这个问题，特提供下面的解题思路．

这组单项式的系数的符号，绝对值规律是什么？

这组单项式的次数的规律是什么？

根据上面的归纳，你可以猜想出第个单项式是什么？

请你根据猜想，请写出第个，第个单项式．

【题目】小华同学经过调查，了解到某客车租赁公司有,两种型号的客车，并得到了下表中的信息.

（1）求每辆型和型客车每天的租金各是多少元？

（2）小华所在学校准备组织七年级全体学生外出一天进行研学活动，小华同学设计了下面甲乙两种租车方案：

方案甲：只租用型客车，但有一辆客车会空出30个座位.

方案乙：只租用型客车，刚好坐满，且比方案甲少用两辆客车.

求小华所在学校七年级学生的总人数.

（3）如果从节省费用的角度考虑，是否还有其他租车方案？如果有，请直接写出一种租车方案；如果没有，请说明理由。

（1）若该班只购买甲种文件夹，且购买甲种文件夹的花费（单位：元）与其购买数量（单位：件）满足一次函数关系，若购买20个，需花费180元；若购买30个，需花费260元.该班若需购买甲种文件夹60件，求需花费多少元？

（2）若该班购买甲，乙两种文件夹，那么甲种文件夹的单价比乙种文件夹的单价贵2元，若用240元购买甲种文件夹的数量与用180元购买乙种文件夹的数量相同.求该文具店甲乙两种文件夹的单价分别是多少元？

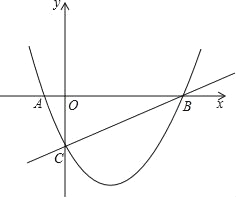
【题目】如图，已知抛物线y=ax2﹣x+c与x轴相交于A、B两点，并与直线y=x﹣2交于B、C两点，其中点C是直线y=x﹣2与y轴的交点，连接AC．

（1）求抛物线的解析式；

（2）证明：△ABC为直角三角形；

（3）△ABC内部能否截出面积最大的矩形DEFG？（顶点D、E、F、G在△ABC各边上）若能，求出最大面积；若不能，请说明理由．

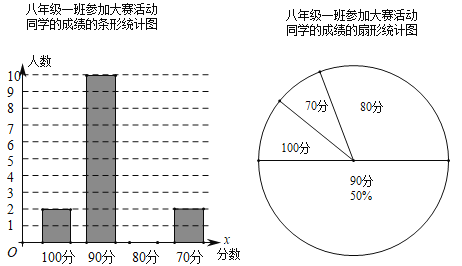
请根据以上提供的信息，解答下列问题：

（1）该校八年级（1）班参加诗词大赛成绩的众数为______分；并补全条形统计图.

（2）求该校八年级（1）班参加诗词大赛同学成绩的平均数；

（3）结合平时成绩、期中成绩和班级预选成绩（如下表），年级拟从该班小何和小王的两位同学中选一名学生参加区级决赛，按的比例计算两位同学的最终得分，请你根据计算结果确定选谁参加区级决赛.

【题目】已知，直线与反比例函数交于点，且点的横坐标为4，过轴上一点作垂直于交于点，如图.

（1）若点是线段上一动点，过点作，，垂足分别于、，求线段长度的最小值.

（2）在（1）的取得最小值的前提下，将沿射线平移，记平移后的三角形为，当时，在平面内存在点，使得、、、四点构成平行四边形，这样的点有几个？直接写出点的坐标.

【题目】如图，正比例函数的图象与反比例函数的图象交于A、B两点，过点A作AC垂直x轴于点C，连结BC．若△ABC的面积为2．

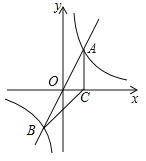
（1）求k的值；

（2）x轴上是否存在一点D，使△ABD为直角三角形？若存在，求出点D的坐标；若不存在，请说明理由．