
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
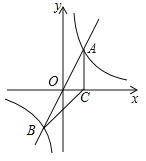
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】(1)k=2;(2)D(5,0)或(﹣5,0)或(![]() ,0)或D(
,0)或D(![]() ,0).
,0).
【解析】试题分析:(1)首先根据反比例函数与正比例函数的图象特征,可知A、B两点关于原点对称,则O为线段AB的中点,故△BOC的面积等于△AOC的面积,都等于1,然后由反比例函数![]() 的比例系数k的几何意义,可知△AOC的面积等于
的比例系数k的几何意义,可知△AOC的面积等于![]() ,从而求出k的值;
,从而求出k的值;
(2)先将![]() 与
与![]() 联立成方程组,求出A、B两点的坐标,然后分三种情况讨论:①当AD⊥AB时,求出直线AD的关系式,令y=0,即可确定D点的坐标;②当BD⊥AB时,求出直线BD的关系式,令y=0,即可确定D点的坐标;③当AD⊥BD时,由O为线段AB的中点,可得OD=
联立成方程组,求出A、B两点的坐标,然后分三种情况讨论:①当AD⊥AB时,求出直线AD的关系式,令y=0,即可确定D点的坐标;②当BD⊥AB时,求出直线BD的关系式,令y=0,即可确定D点的坐标;③当AD⊥BD时,由O为线段AB的中点,可得OD=![]() AB=OA,然后利用勾股定理求出OA的值,即可求出D点的坐标.
AB=OA,然后利用勾股定理求出OA的值,即可求出D点的坐标.
试题解析:(1)∵反比例函数与正比例函数的图象相交于A、B两点,∴A、B两点关于原点对称,∴OA=OB,∴△BOC的面积=△AOC的面积=2÷2=1,又∵A是反比例函数![]() 图象上的点,且AC⊥x轴于点C,∴△AOC的面积=
图象上的点,且AC⊥x轴于点C,∴△AOC的面积=![]() ,∴
,∴![]() ,∵k>0,∴k=2.故这个反比例函数的解析式为
,∵k>0,∴k=2.故这个反比例函数的解析式为![]() ;
;
(2)x轴上存在一点D,使△ABD为直角三角形.将![]() 与
与![]() 联立成方程组得:
联立成方程组得: 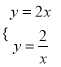 ,解得:
,解得: ![]() ,
, ![]() ,∴A(1,2),B(﹣1,﹣2),
,∴A(1,2),B(﹣1,﹣2),
①当AD⊥AB时,如图1,
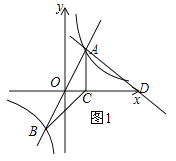
设直线AD的关系式为![]() ,将A(1,2)代入上式得:
,将A(1,2)代入上式得: ![]() ,∴直线AD的关系式为
,∴直线AD的关系式为![]() ,令y=0得:x=5,∴D(5,0);
,令y=0得:x=5,∴D(5,0);
②当BD⊥AB时,如图2,
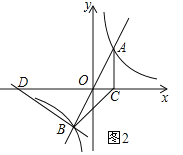
设直线BD的关系式为![]() ,将B(﹣1,﹣2)代入上式得:
,将B(﹣1,﹣2)代入上式得: ![]() ,∴直线AD的关系式为
,∴直线AD的关系式为![]() ,令y=0得:x=﹣5,∴D(﹣5,0);
,令y=0得:x=﹣5,∴D(﹣5,0);
③当AD⊥BD时,如图3,
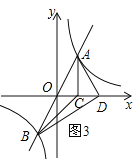
∵O为线段AB的中点,∴OD=![]() AB=OA,∵A(1,2),∴OC=1,AC=2,由勾股定理得:OA=
AB=OA,∵A(1,2),∴OC=1,AC=2,由勾股定理得:OA=![]() =
=![]() ,∴OD=
,∴OD=![]() ,∴D(
,∴D(![]() ,0),
,0),
根据对称性,当D为直角顶点,且D在x轴负半轴时,D(![]() ,0);
,0);
故x轴上存在一点D,使△ABD为直角三角形,点D的坐标为(5,0)或(﹣5,0)或(![]() ,0)或D(
,0)或D(![]() ,0).
,0).


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】已知点P(-3,m)和Q(1,m)都在二次函数y=2x2+b x-1的图像上.
(1)求b、m的值;
(2)将二次函数图像向上平移几个单位后,得到的图像与x轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年1月19日,国家统计局公布了2015年宏观经济数据,初步核算,全年国内生产总值为676000亿元.676000用科学记数法表示为( )
A.6.76×106
B.6.76×105
C.67.6×105
D.0.676×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com