
科目: 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了庆祝元旦,学校准备举办一场“经典诵读”活动,某班准备网购一些经典诵读本和示读光盘,诵读本一套定价100元,示读光盘一张定价20元.元旦期间某网店开展促销活动,活动期间向客户提供两种优惠方案:
方案A:买一套诵读本送一张示读光盘;
方案B:诵读本和示读光盘都按定价的九折付款.
现某班级要在该网店购买诵读本10套和示读光盘x张(x>10),解答下列三个问题:
(1)若按方案A购买,共需付款 元(用含x的式子表示),
若按方案B购买,共需付款 元(用含x的式子表示);
(2)若需购买示读光盘15张(即x=15)时,请通过计算说明按哪种方案购买较为合算;
(3)若需购买示读光盘15张(即x=15)时,你还能给出一种更为省钱的购买方法吗?若能,请写出你的购买方法和所需费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.
(1)改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元?
(2)已知改造1个甲种型号大棚的时间是5天,改造1个乙种型号大概的时间是3天,该基地计划改造甲、乙两种蔬菜大棚共8个,改造资金最多能投入128万元,要求改造时间不超过35天,请问有几种改造方案?哪种方案基地投入资金最少,最少是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下面的几个算式:
1+2+1=4=2×2;1+2+3+2+1=9=3×3;
1+2+3+4+3+2+1=16=4×4;![]() 。
。
根据上面几道题的规律,计算下面的题:
1+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1的值为__________
查看答案和解析>>
科目: 来源: 题型:
【题目】某单位组织职工开展植树活动,植树量与人数之间的关系如图20-1-1所示,由图可知参加本次植树活动的共有______人,他们总共植树______棵,平均每人植树_____棵(结果精确到0.01).
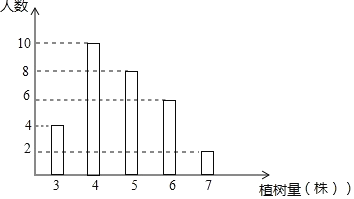
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线l:y1=﹣![]() x﹣1与y轴交于点A,一次函数y2=
x﹣1与y轴交于点A,一次函数y2=![]() x+3图象与y轴交于点B,与直线l交于点C.
x+3图象与y轴交于点B,与直线l交于点C.
(1)画出一次函数y2=![]() x+3的图象;
x+3的图象;
(2)求点C坐标;
(3)如果y1>y2,那么x的取值范围是______.
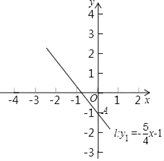
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是正方形,在AB的延长线上取一点E,连接EC,过点C作CF⊥EC交AD于F.
(1)求证:EC=FC.
(2)若G、M分别是AB、CD上一动点,连接GM.H是GM上的中点,连接BH,当G、M运动到某一特殊位置时得到BH=BG +CM,此时∠ABH的度数是多少?请说明理由.
(3)在(2)的条件下,若BG=1,MC=![]() ,连接AH.求出四边形AHMD的面积.
,连接AH.求出四边形AHMD的面积.
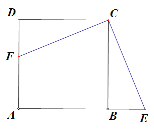
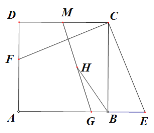
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列一段文字:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2)),M,N两点之间的距离可以用公式MN=![]() 计算.解答下列问题:
计算.解答下列问题:
(1)若点P(2,4),Q(﹣3,﹣8),求P,Q两点间的距离;
(2)若点A(1,2),B(4,﹣2),点O是坐标原点,判断△AOB是什么三角形,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
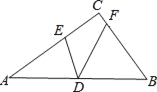
【题目】如图,在△ABC中,∠ACB=90°,D为边AB的中点,E,F分别为边AC,BC上的点,且AE=AD,BF=BD.若DE=2![]() ,DF=4,则AB的长为_____.
,DF=4,则AB的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com