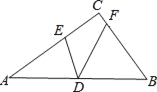
【题目】如图，在△ABC中，∠ACB=90°，D为边AB的中点，E，F分别为边AC，BC上的点，且AE=AD，BF=BD．若DE=2
，DF=4，则AB的长为_____．
【答案】4
【解析】如图，延长FD到M使得DM=DF，连接AM、EM、EF，作EN⊥DF于N．∵AE=AD，BF=BD，∴∠AED=∠ADE，∠BDF=∠BFD，∴2∠ADE+∠BAC=180°，2∠BDF+∠B=180°，∴2∠ADE+2∠BDF=270°，∴∠ADE+∠BDF=135°，∴∠EDF=180°﹣（∠ADE+∠BDF）=45°，∵∠END=90°，DE=2
，∴∠EDN=∠DEN=45°，∴EN=DN=2，在△DAM和△DBF中，DA=DB，∠ADM=∠BDF，DM=DF，∴△ADM≌△BDF，∴BF=AM=BD=AD=AE，∠MAD=∠B，∴∠MAE=∠MAD+∠BAC=90°，∴EM=
AM，在RT△EMN中，∵EN=2，MN=DM+DN=6，∴EM=
=2
，∴AM=2
，AB=2AM=4
，故答案为4
．
天天练口算系列答案科目：初中数学 来源： 题型：
【题目】计算下列各题：（1）
_______；（2）
________；
（3）
_______；（4）
_______；
（5）
________；（6）
________.
查看答案和解析>>
科目：初中数学 来源： 题型：
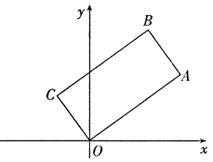
【题目】如图，在矩形
中， 
，顶点
在坐标原点，顶点
的坐标为(8,6).
(1)顶点
的坐标为( ， )，顶点
的坐标为( ， );
(2)现有动点
、
分别从
、
同时出发，点
沿线段
向终点
运动，速度为每秒2个单位，点
沿折线
→
→
向终点
运动，速度为每秒
个单位.当运动时间为2秒时，以点
、
、
顶点的三角形是等腰三角形，求
的值.
(3)若矩形
以每秒
个单位的速度沿射线
下滑，直至顶点
到达坐标原点时停止下滑.设矩形
在
轴下方部分的面积为
，求
关于滑行时间
的函数关系式，并写出相应自变量
的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
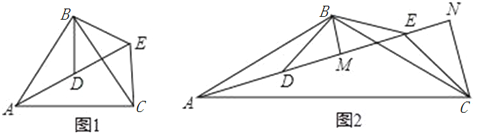
【题目】如图，△ABC和△DBE均为等腰三角形，点A，D，E在同一直线上，连接CE．
（1）如图1，若∠BAC=∠BCA=∠BDE=∠BED=55°
①求证：AD=CE；
②求∠AEC的度数．
（2）如图2，若∠ABC=∠DBE=120°，BM为△BDE中DE边上的高，CN为△ACE中AE边上的高，
试证明：AE=
．
查看答案和解析>>
科目：初中数学 来源： 题型：
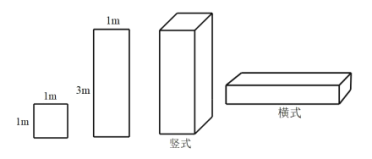
【题目】某工厂准备用图甲所示的
型正方形板材和
型长方形板材，制作成图乙所示的竖式和横式两种无盖箱子.
（1）若该工厂准备用不超过2400元的资金去购买，两种型号板材，制作竖式、横式箱子共10个，已知型板材每张20元，型板材每张60元，问最多可以制作竖式箱子多少只？
（2）若该工程新购得65张规格为
型正方形板材，将其全部切割测好难过型或型板材（不计损耗），用切割的板材制作两种类型的箱子，要求竖式箱子不少于10只，且材料恰好用完，则能制作竖式箱子______只.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下面的几个算式：
1＋2＋1＝4＝2×2；1＋2＋3＋2＋1＝9＝3×3；
1＋2＋3＋4＋3＋2＋1＝16＝4×4；
。
根据上面几道题的规律，计算下面的题：
1＋2＋3＋4＋5＋6＋7＋8＋9＋8＋7＋6＋5＋4＋3＋2＋1的值为__________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】求一个正数的算术平方根，有些数可以直接求得，如
，有些数则不能直接求得，如
，但可以通过计算器求得，还可以通过一组数的内在联系，运用规律求得.请同学们观察下表：
| 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
（1）表中所给的信息中，你能发现什么规律？（请将规律用文字表述出来）
（2）运用你发现的规律，探究下列问题：已知
，求下列各数的算术平方根：
①0.0206；②2060000.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有一个水池，其底面是边长为16尺的正方形，一根芦苇AB生长在它的正中央，高出水面部分BC的长为2尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′，则这根芦苇AB的长是（ ）
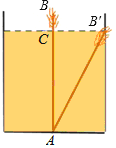
A. 15尺B. 16尺C. 17尺D. 18尺
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知a是不为1的有理数，我们把
称为a的差倒数，如2的差倒数是
=-1.现已知a1=
,a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数.
（1）求a2,a3,a4的值.
（2）根据（1）的计算结果，请猜想并写出a2018·a2019·a2020的值.
（3）计算：a1+a2+a3+…+a2018+a2019.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
