
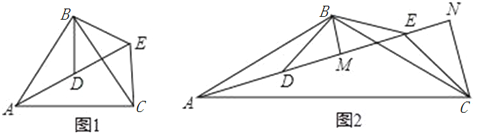
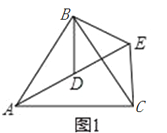
【题目】如图,△ABC和△DBE均为等腰三角形,点A,D,E在同一直线上,连接CE.
(1)如图1,若∠BAC=∠BCA=∠BDE=∠BED=55°
①求证:AD=CE;
②求∠AEC的度数.
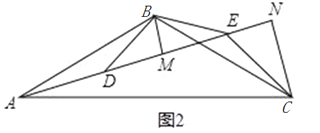
(2)如图2,若∠ABC=∠DBE=120°,BM为△BDE中DE边上的高,CN为△ACE中AE边上的高,![]() 试证明:AE=
试证明:AE=![]() .
.
【答案】(1)①证明见解析②70°(2)![]()
【解析】(1)关键全等三角形的判定方法,判断出△BAD≌△CAE,即可判断出BD=CE.
(2)①首先根据△ACB和△CE均为等腰三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为90°即可;
解:(1)证明:∵∠ABD+∠DBC=∠CBE+∠DBC=55°,
∴∠ABD=∠CBE.
∵△ABC和△DBE均为以点B为腰上顶点的等腰三角形.
∴BA=BC,BD=BE
∴△ABD≌△CBE.
∴AD=CE
②:解:∵△ABD≌△CBE(已证)
∴∠BDA=∠BEC=180°-∠BDE
∵∠AEC=∠BEC-∠BED
∴∠AEC =180°-2∠BDE=70°
(2)同理可证:AD=CE,∠AEC=120° ,∴∠CEN=60°,
∵CN为△ACE中AE边上的高,
∴∠ECN=30°,∵CN=a,![]()
根据勾股定理:CE=![]() ,
,
∴AD=CE=![]() ,
,![]()
∵△DBE为等腰三角形, BM为△BDE中DE边上的高
∴DE=2DM,
∵∠DBE=120°,∴∠BDM=30°,
∴根据勾股定理:DM=![]() ,
,![]()
∴DE=2DM=2![]()
![]() ,
,
∴AE=AD+DE=![]() +2
+2![]()
![]()
“点睛”此题主要考查了全等三角形的判定方法和性质,等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:在判定三角形全等时,关键是选择恰当的判定条件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】对于二次函数![]() ,有下列说法:
,有下列说法:
①如果![]() =2,则
=2,则![]() 有最小值-1; ②如果当
有最小值-1; ②如果当![]() 时
时![]() 随
随![]() 的增大而减小,则
的增大而减小,则![]() =1;
=1;
③如果将它的图象向左平移3个单位后的函数的最小值是-9,则![]() ;
;
④如果当![]() =1时的函数值与
=1时的函数值与![]() =2015时的函数值相等,则当
=2015时的函数值相等,则当![]() =2016时的函数值为3.其中正确的说法是_____________.(把你认为正确的结论的序号都填上)
=2016时的函数值为3.其中正确的说法是_____________.(把你认为正确的结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
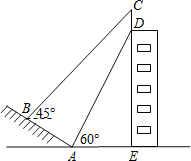
【题目】如图,山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:
,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC与三角形![]() 在平面直角坐标系中的位置如图所示,三角形
在平面直角坐标系中的位置如图所示,三角形![]() 是由三角形ABC经过平移得到的.
是由三角形ABC经过平移得到的.
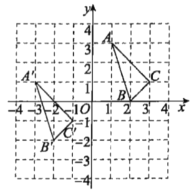
(1)分别写出点![]()
![]()
![]() 的坐标;
的坐标;
(2)说明三角形![]() 是由三角形ABC经过怎样的平移得到的;
是由三角形ABC经过怎样的平移得到的;
(3)若点![]() 是三角形ABC内的一点,则平移后点P在三角形
是三角形ABC内的一点,则平移后点P在三角形![]() 内的对应点为P‘,写出点P’的坐标.
内的对应点为P‘,写出点P’的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.

(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠DPF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年(4)班要举行一场毕业联欢会,主持人同时转动下图中的两个转盘,由一名同学在转动前来判断两个转盘上指针所指的两个数字之和是奇数还是偶数,如果判断错误,他就要为大家表演一个节目;如果判断正确,他可以指派别人替自己表演节目.现在轮到小明来选择,小明不想自己表演,于是他选择了偶数.
小明的选择合理吗?从概率的角度进行分析(要求用树状图或列表方法求解)

查看答案和解析>>
科目:初中数学 来源: 题型:
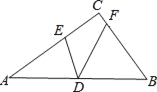
【题目】如图,在△ABC中,∠ACB=90°,D为边AB的中点,E,F分别为边AC,BC上的点,且AE=AD,BF=BD.若DE=2![]() ,DF=4,则AB的长为_____.
,DF=4,则AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
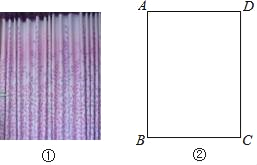
【题目】如图①,窗帘的褶皱是指按照窗户的实际宽度将窗帘布料以一定比例加宽的做法,褶皱之后的窗帘更能彰显其飘逸、灵动的效果.其中,窗宽度的1.5倍为平褶皱,窗宽度的2倍为波浪褶皱.如图②,小莉房间的窗户呈长方形,窗户的宽度(AD)比高度(AB)的少0.5m,某种窗帘的价格为120元/m2.如果以波浪褶皱的方式制作该种窗帘比以平褶皱的方式费用多180元,求小莉房间窗户的宽度与高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上一动点,点Q为边AC上一动点,且∠PDQ=90°.

(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为点F,若△PDF为等腰三角形,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com